Interferencias de Ondas

Cuando en lugar de una onda, tenemos dos o más propagándose en el mismo medio, y estas se cruzan en un punto, dichas ondas interfieren. En este apartado vamos a estudiar las interferencias de ondas, particularizando para el caso de las producidas por perturbaciones armónicas. En este apartado vamos a estudiar:

• Qué entendemos exactamente por interferencia en Física
• La ecuación resultante de una interferencia de dos ondas armónicas, a partir del principio de superposición
• Cómo clasificamos las interferencias

Si no hay ninguna interferencia que te distraiga, vamos a empezar...

Concepto

Para entender con claridad qué son las interferencias de ondas te proponemos comenzar con un ejemplo facilmente reproducible: lanza dos piedras a la vez en un estanque en calma. Observa que las ondas generadas por cada piedra se entrecruzan para seguir posteriormente cada una su camino. Sin embargo, en los puntos de interesección de las ondas habrá zonas con una amplitud mayor y zonas con una amplitud menor de la que tendria cada onda individualmente. Decimos que en tales puntos, en los que las ondas se superponen, se producen interferencias.

Interferencias en un estanque

Cuando dos o más ondas provocadas en puntos distintos se cruzan en el agua se forman interferencias.

Observa que, a diferencia de lo que ocurre con los cuerpos rígidos, varias ondas pueden pasar simultáneamente por el mismo punto. Así mismo, una vez que se ha producido la interferencia, los movimientos ondulatorios continúan su propagación separadamente, sin experimentar ninguna modificación ni en la energía ni en la cantidad de movimiento que tenían antes de la interferencia.

Pero, ¿cómo podemos describir matemáticamente una interferencia? Como quizás ya habrás podido intuir, las interferencias se rigen por el principio de superposición.

Superposición de ondas

Matemáticamente el fenómeno de las interferencias puede ser descrito gracias al principio de superposición: Las ondas individuales se combinan entre sí en una región del espacio para producir una onda resultante.

La afirmación anterior quiere decir que si, por ejemplo, consideramos dos ondas mecánicas y un punto P tenía que desplazarse verticalmente +2 cm debido a la primera onda y -3 cm debido a una segunda, el paso simultáneo de las dos ondas, su interferencia, hará que dicho punto se desplace +2 - 3 = -1 cm. La siguiente imagen ilustra esta idea.

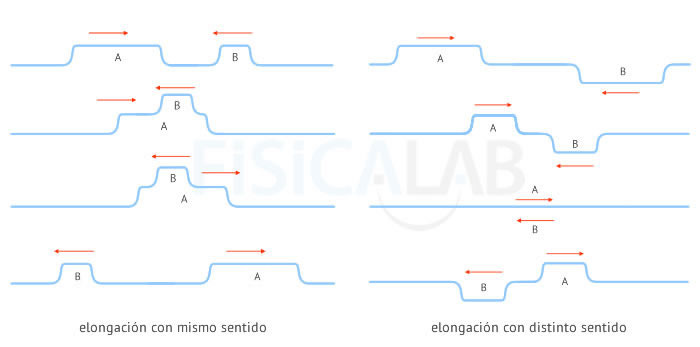
Superposición de Ondas

La imagen superior ilustra distintos instantes de la propagación de dos pulsos de onda (A y B) sobre un mismo medio, una cuerda. En la primera columna, a la izquierda, se pueden observar los efectos cuando las elongaciones de los pulsos tienen igual sentido, y en la segunda, a la derecha, lo que ocurre cuando tienen sentido opuesto. En aquellos puntos en los que las ondas se encuentran, en la instantánea 2ª y 3ª  de cada columna, el desplazamiento respecto a la posición de equilibrio experimentado es la suma de los que la cuerda experimentaría de manera individual, si sólo se propagase una de las ondas.

Los fenómenos de interferencia son, en general, complejos. En este nivel vamos a centrarnos en el estudio de ondas armónicas que tienen igual amplitud, frecuencia angular y número de onda y que están en fase , o cuya diferencia de fase es constante en el tiempo (ondas coherentes). Si deseas consultar variaciones al desarrollo que vamos a presentarte, consulta los ejercicios de este apartado.

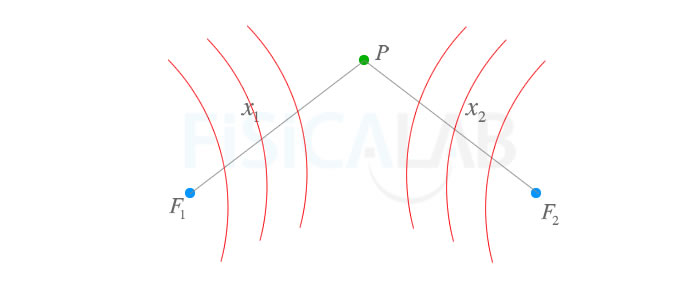
Interferencia de ondas coherentes

En el punto P interfieren dos ondas coherentes, tras haber recorrido una distancia x₁ y x₂ desde sus focos F₁ y F₂ respectivamente. Supondremos que la amplitud con la que ambas ondas llegan a dicho punto es las misma: A.

Vamos a estudiar la vibración resultante en el punto P. Para ello, consideraremos la aportación a dicha vibración que realiza cada onda individualmente, en nuestro caso y₁ e y₂. Se trata, en definitiva, de fijar x en la ecuación general de cada onda armónica, y obtener su elongación y correspondiente:

$$\left.\begin{array}{r}{y}_1=A·sin\left(\omega ·t-k·x_1\right)\\ y_2=A·sin\left(\omega ·t-k·x_2\right)\end{array}\right\}$$

Si sumamos ambas, según el principio de superposición, obtenemos:

$$y_T=y_1+y_2=A·\left(\sin \left(\omega ·t-k·x_1\right)+sin\left(\omega ·t-k·x_2\right)\right)$$

Ahora, debemos tener en cuenta que:

$$\sin \left(A\right)+\sin \left(B\right)=2·\cos \left(\frac{A-B}{2}\right)·\sin \left(\frac{A+B}{2}\right)$$

Con lo que podemos escribir:

$$y_T=2·A·\cos \left(\frac{k·\left(x_2-x_1\right)}{2}\right)·\sin \left(\frac{2·\omega ·t-k·\left(x_1+x_2\right)}{2}\right)=\underset{A_T}{\underbrace{2·A·\cos \left(\frac{k·\left(x_2-x_1\right)}{2}\right)}}·sin\left(\omega ·t-k·\frac{x_1+x_2}{2}\right)$$

Observa que al factor $2·A·cos\left(\frac{k·\left(x_2-x_1\right)}{2}\right)$ , que no depende del tiempo, lo llamamos A_T.

Amplitud resultante

El valor de la amplitud resultante A_T , expresado en función de las distancias a los focos x₁ y x₂ , puede ser reescrito para relacionarlo con la longitud de onda y con la diferencia de fase entre las ondas originales. Efectivamente:

$$k·\frac{x_2-x_1}{2}=\frac{2·\pi }{\lambda }·\frac{x_2-x_1}{2}=\frac{\pi }{\lambda }·\left(x_2-x_1\right)$$

Y, por otro lado:

$$k·\frac{x_2-x_1}{2}=\frac{1}{2}·\left(∆\phi \right)$$ 

...ya que...

$$k·\frac{x_2-x_1}{2}=k·\frac{x_2}{2}-k·\frac{x_1}{2}+\frac{\omega ·t}{2}-\frac{\omega ·t}{2}=\frac{1}{2}·\left(\left(\omega ·t-k·x_1\right)-\left(\omega ·t-k·x_2\right)\right)=\frac{1}{2}·\left({\phi }_1-{\phi }_2\right)=\frac{1}{2}·\left(∆\phi \right)$$

Con lo que podemos concluir que:

Por tanto, si nos centramos en observar qué ocurre en el punto P de interferencia, podemos concluir que este vibrará según un movimiento armónico simple cuya amplitud dependerá de las distancias x₁ y x₂ de P a los focos. Esto da lugar a que podamos distinguir fundamentalmente dos tipos de interferencia: constructivas y destructivas.

Experimenta y Aprende

Cargando...

Interferencia de ondas

Cuando dos o más ondas se propagan en un mismo medio y coinciden en un punto, se produce en este una interferencia. Pulsa sobre el botón play para comenzar a experimentar.

Tipos de Interferencia

Atendiendo a la amplitud de la vibración resultante en el punto de interferencia, podemos clasificar las interferencias en constructivas y destructivas. Observa que una interferencia es constructiva o destructiva según el punto considerado, siendo, en general, constructivas en unos puntos y destructivas en otros.

Por otro lado, ten presente que, aunque en las comprobaciones realizadas a continuación hemos supuesto que las ondas que interfieren tienen igual frecuencia y amplitud, las condiciones de interferencia constructiva y destructiva son válidas también cuando las ondas tienen distinta amplitud, salvo que, en este último caso, la interferencia destructiva no llega nunca a anular completamente la amplitud.

Interferencia constructiva

Comprobación

Ya hemos indicado que la vibración en el punto de interferencia tiene una amplitud cuya expresión es $A_T=2·A·\cos \left(\frac{∆\phi }{2}\right)=2·A·\cos \left(\frac{2·\pi }{\lambda }·\left(x_2-x_1\right)\right)$ , con lo que los valores de amplitud máxima, A_T = ±2·A, se producirán cuando $\cos \left(\frac{∆\phi }{2}\right)=\pm 1$ ,o cuando  $cos\left(\frac{\pi }{\lambda }·\left(x_2-x_1\right)\right)=\pm 1$ . De la primera condición, podemos concluir que se producirá una interferencia constructiva cuando las ondas estén en fase:

$$\frac{∆\phi }{2}=n·\pi \Rightarrow ∆\phi =2·n·\pi$$

Y de la segunda, que eso se produce cuando la diferencia entre las distancias al foco es múltiplo entero de la longitud de onda:

$$\frac{\pi }{\lambda }·\left(x_2-x_1\right)=n·\pi \Rightarrow x_2-x_1=n·\lambda$$

Interferencia destructiva

Comprobación

Ya hemos indicado que la vibración en el punto de interferencia tiene una amplitud cuya expresión es $A_T=2·A·\cos \left(\frac{∆\phi }{2}\right)=2·A·\cos \left(\frac{2·\pi }{\lambda }·\left(x_2-x_1\right)\right)$ , con lo que los valores de amplitud mínima, A_T=0, se producirán cuando $\cos \left(\frac{∆\phi }{2}\right)=0$ ,o cuando  $cos\left(\frac{\pi }{\lambda }·\left(x_2-x_1\right)\right)=0$ . De la primera condición, podemos concluir que se producirá una interferencia destructiva cuando las ondas estén en oposición de fase:

$$\frac{∆\phi }{2}=n·\pi +\frac{\pi }{2}\Rightarrow ∆\phi =\left(2·n+1\right)·\pi$$

Y de la segunda, que eso se produce cuando la diferencia entre las distancias al foco es múltiplo impar de la semilongitud de onda:

$$\frac{\pi }{\lambda }·\left(x_2-x_1\right)=n·\pi +\frac{\pi }{2}\Rightarrow x_2-x_1=\left(2·n+1\right)·\frac{\lambda }{2}$$