Energía, Potencia e Intensidad de Ondas

El movimiento ondulatorio se define como una perturbación que se propaga capaz de transportar energía sin la necesidad de transportar materia. Esta propagación de energía en las ondas se pone claramente de manifiesto en distintos fenómenos de la naturaleza, a veces de manera dramática, como el caso de las ondas sísmicas que generan los terremotos. Otras veces, en cambio, constituye la base de la vida en la Tierra, como es el caso de la energía propagada por la luz procedente del Sol.

La cara y la cruz de las ondas

El desplazamiento de las placas tectónicas puede dar lugar a terremotos. Las ondas sísmicas generadas transportan energía cuyos efectos pueden llegar a ser devastadores. Por otro lado, la energía que llega en forma de luz solar a la Tierra es imprescindible para que los seres vivos puedan realizar su ciclo vital.

Un ejemplo fácilmente reproducible se da cuando arrojamos una piedra a un estanque de aguas calmadas. Las ondas generadas en la superficie son capaces de transmitir su energía a un trozo de corcho inicialmente en reposo a cierta distancia del foco, y hacer que este describa un movimiento oscilatorio. En este apartado vamos a cuantificar la energía que es capaz de transferir el movimiento ondulatorio. Nos centraremos en el caso de una onda mecánica y armónica que se transmite en un medio sin pérdidas, y seguiremos el siguiente orden :

• Presentaremos la energía transmitida en ondas...
  • unidimensionales
  • bidimensionales
  • tridimensionales
• Introduciremos el concepto de potencia de una onda
• Veremos qué es la intensidad de una onda

¿Estás preparado?

Estudio energético de ondas: una dimensión

Estudiando el comportamiento de una onda sencilla, como lo es aquella que se propaga en una dimensión, podemos llegar a una conclusión importante.

Comprobación

Para comprobar la afirmación anterior particularizaremos para el caso de una cuerda unida en uno de sus extremos a un oscilador armónico como el de la figura. Sabemos que a consecuencia del movimiento del oscilador (el foco) se producirá en la cuerda una onda unidimensional, armónica y transversal que se desplazará hacia la derecha haciendo que cualquier punto de la misma "se solidarice" y siga, igualmente, un m.a.s.

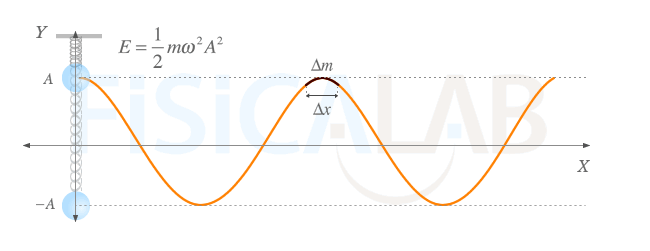
Energía transmitida por una onda

El oscilador armónico de la figura, atado a una cuerda, hace que cada partícula de la misma oscile siguiendo un movimiento armónico simple de características similares a las del foco, pero con cierto retraso respecto a este, según la velocidad de propagación que tenga la onda sobre la cuerda.  A una porción de masa ∆m le corresponde un segmento de longitud ∆x.

La energía que tiene el oscilador que actúa de foco viene dada por:

$$E_{osc}=\frac{1}{2}·m_{osc}·{{\omega }_{osc}}^2·{A_{osc}}^2$$ 

Por otro lado, dado que una porción cualquiera de la cuerda, de masa ∆m y que abarque una longitud ∆x, también oscila según un m.a.s., podemos escribir que la energía que tendrá dicha porción será:

$$∆E=\frac{1}{2}·∆m·{\omega }^2·A^2$$

Ahora bien, podemos definir ρ como la densidad lineal, es decir, la masa por unidad de longitud, quedando entonces:

$$\mu =m/x\Rightarrow ∆m=\mu ·∆x$$

La energía de una porción de cuerda queda, reescribiendo la expresión anterior:

$$∆E=\frac{1}{2}·\mu ·∆x·{\omega }^2·A^2$$

La expresión anterior corresponde a la energía en un segmento de cuerda de longitud ∆x. Podemos elegir como longitud la longitud de onda λ, quedando la energía contenida en una longitud de onda:

$$E=\frac{1}{2}·\mu ·\lambda ·{\omega }^2·A^2\underset{\left[1\right]}{=}2·{\mathrm{\pi }}^2·\mu ·\lambda ·f^2·A^2$$

Donde en [1] hemos usado que ω=2·π·f. Como vemos, pues, esto es justamente lo que queríamos comprobar, es decir, que $E=cte·f^2·A^2$ .

Estudio energético de ondas en dos dimensiones

Para abordar el estudio de las ondas bidimensionales nos centraremos en el caso de una onda con un frente de ondas circular que se propaga en un medio homogéneo e isótropo.

Comprobación

Para comprobar la afirmación anterior recurriremos al clásico ejemplo de propagación de una onda sobre la superficie de un estanque en calma. En esta ocasión, sin embargo, en lugar de considerar una piedra que cae, consideraremos que hay un oscilador armónico como fuente del movimiento.

Onda en un estanque

Una onda propagándose en la superficie de un estanque es un ejemplo de frente circular propagándose en un medio isótropo.

La energía del oscilador, como ocurría antes, será la que se transmita al medio y viene dada por:

$$E_{osc}=\frac{1}{2}·m_{osc}·{{\omega }_{osc}}^2·{A_{osc}}^2$$

Sin embargo, en esta ocasión, la conservación de la energía exige que esta se transmita, no linealmente, de partícula en partícula adyacente, como ocurría antes, sino circularmente, a través de las muchas partículas que constituyen los sucesivos frentes de ondas que se van formando. Dicho de otro modo, la energía de dos frentes de ondas cualesquiera es la misma.

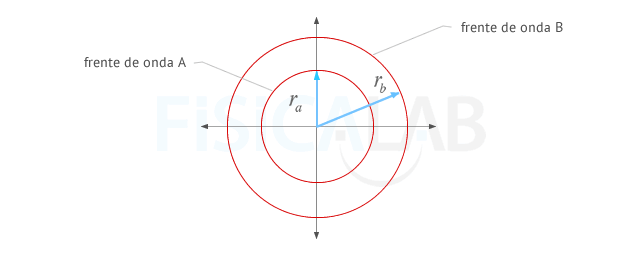
Energía en frentes de onda bidimensionales

La energía de los frentes de onda a, situado a una distancia r_a del foco, y b situado a r_b es la misma ya que la energía "que suministra" el foco se distribuye por todo el frente.

Para determinar la energía de un frente de ondas completo, consideraremos:

• Que cada partícula individual del frente se comporta como un oscilador armónico

• Que todo el frente, en su conjunto, también se comporta como oscilador armónico ya que todas las partículas del mismo vibran al unísono

• Que podemos observar fácilmente como a medida que el frente de ondas se encuentra más alejado del foco, la amplitud de oscilación decrece

• Que la longitud de un frente genérico situado a una distancia r_a del origen es l_a=2·π·r_a

• Que podemos determinar la masa del frente en su conjunto en función de la densidad lineal del medio μ=m/l (masa por unidad de longitud) según $\mu =m/l\Rightarrow m=\mu ·2·\mathrm{\pi }·r_a$ 

Con lo que podemos escribir:

$$E_{frent{e}_a}=\frac{1}{2}·m_{frent{e}_a}·{\omega }^2·{A_a}^2=\frac{1}{2}·\mu ·2·\mathrm{\pi }·r_a·{\omega }^2·{A_a}^2$$ 

Siguiendo un razonamiento similar para un frente a una distancia r_b del foco nos quedaría:

$$E_{frent{e}_b}=\frac{1}{2}·\mu ·2·\mathrm{\pi }·r_b·{\omega }^2·{A_b}^2$$

Donde hemos tenido en cuenta que la frecuencia angular ω de ambos frentes es la misma, ya que esta queda fijada por la frecuencia del foco. Finalmente, dado que la energía debe conservarse, podemos escribir:

$$E_{frent{e}_a}=E_{frent{e}_b}=cte\Rightarrow r_a·{A_a}^2=r_b·{A_b}^2=cte$$

Podemos generalizar la expresión anterior escribiendo:

$$r·A^2=cte\Rightarrow A=\frac{cte}{\sqrt{r}}\Rightarrow \boxed{A\propto \frac{1}{\sqrt{r}}}$$

Que es justamente lo que queríamos comprobar.

El desarrollo anterior también guarda otra expresión de gran utilidad para los ejercicios. Efectivamente, conocida la amplitud A_a de una onda circular a una determinada distancia r_a del foco, podemos determinar la amplitud A_b a cualquier otra distancia r_b según la relación:

$$\boxed{r_a·{A_a}^2=r_b·{A_b}^2}$$

Estudio energético de ondas en tres dimensiónes

Para abordar el estudio de las ondas triidimensionales nos centraremos en el caso de una onda esférica que se propaga de nuevo en un medio homogéneo e isótropo.

Comprobación

Para comprobar la afirmación procederemos de manera análoga al ejemplo de ondas en dos dimensiones, pero en este caso tendremos en cuenta que los frentes de onda no son líneas circulares sino superficies esféricas. La masa de un frente de ondas, en este caso, se determina a partir de la densidad superficial ρ=m/S (masa por unidad de superficie) y la superficie de la esfera viene dada por S=4·π·r² por lo que m=ρ·4·π·r².

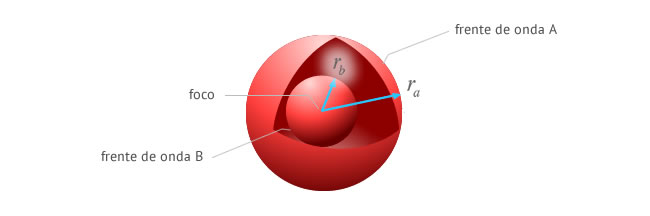
Energía en frentes de onda tridimensionales

La energía de dos frentes de onda cualesquiera de una onda esférica situados a distancias r_a y r_b del origen permanece constante.

La energía de cada uno de los frentes anteriores viene dada por:

$$\begin{gathered} E_{frent{e}_a}=\frac{1}{2}·\rho ·4·\mathrm{\pi }·{r_a}^2·{\omega }^2·{A_a}^2 \\ {E}_{frent{e}_b}=\frac{1}{2}·\rho ·4·\mathrm{\pi }·{r_b}^2·{\omega }^2·{A_b}^2 \end{gathered}$$

Y dado que por la conservación de la energía $E_{frent{e}_a}=E_{frent{e}_b}=cte$ , nos queda:

$$\begin{gathered} {r_a}^2·{A_a}^2={r_b}^2·{A_b}^2=cte\Rightarrow r^2·A^2=cte\Rightarrow A=\frac{cte}{r}\Rightarrow \\ \Rightarrow \boxed{A\propto \frac{1}{r}} \end{gathered}$$ 

Que es justamente lo que queríamos comprobar.

De nuevo, el desarrollo anterior nos regala una expresión para el cálculo de la amplitud A_b de una onda esférica a una determinada distancia r_b del foco, conocida la amplitud A_a a una distancia r_a:

$$\boxed{{r_a}^2·{A_a}^2={r_b}^2·{A_b}^2}$$

Potencia

Comprobación

Para comprobar la expresión anterior podríamos centrarnos en cualquiera de los ejemplos anteriores usados para los casos de ondas unidimensionales, bidimensionales o tridimensionales. Nos centraremos en el caso de la onda transmitiéndose en una dimensión y partiremos de la expresión de su energía y de la definición de potencia como energía por unidad de tiempo. Así, se puede escribir:

$$P=\frac{E}{t}=\frac{2·{\mathrm{\pi }}^2·\mu ·∆x·f^2·A^2}{t}\underset{\left[1\right]}{=}2·{\mathrm{\pi }}^2·\mu ·v·f^2·A^2$$

Donde en [1] hemos usado que v=∆x/t es la velocidad de propagación de la onda sobre la cuerda, constante. Esto es justo lo que queríamos comprobar, es decir, que $P=cte·f^2·A^2$ .

Intensidad

Una magnitud muy relevante para el estudio energético del movimiento ondulatorio de las ondas que se propagan en el espacio es su intensidad.

En el caso de ondas esféricas hemos visto que la amplitud decrece a medida que nos alejamos del foco emisor, por lo que igualmente la intensidad de la onda disminuye a medida que nos alejamos del foco. A esta amortiguación de la onda debida al reparto de energía entre frente de ondas cada vez mayores se le denomina formalmente atenuación y es responsable, por ejemplo, de que si pegas tu oreja al altavoz de tu móvil puedas oír claramente la conversación que serías incapaz de oír, digamos, a 2 metros de este.