Ondas Mecánicas

En función de la clase de energía propagada podemos clasificar las ondas en dos grandes grupos, ondas electromagnéticas y ondas mecánicas. Estas últimas, que propagan energía mecánica, se caracterizan por que requieren de un medio material para propagarse por lo que también se las puede llamar ondas materiales. Ejemplos de estas son el sonido, la onda propagada por la superficie de un estanque o la onda que se propaga cuando agitamos una cuerda o un muelle. En este apartado vamos a profundizar en ellas estudiando:

• Cómo se produce la propagación de las ondas mecánicas
• A qué velocidad se propagan
• Cuál es su ecuación de propagación

¿Empezamos?

Propagación de ondas en medios elásticos

Para que una onda mecánica se pueda propagar el medio debe cumplir dos requisitos fundamentales:

• Ser elástico. Un medio elástico da lugar a la aparición de fuerzas de restauración cuando una parte del mismo se aparta de su posición de equilibrio
• Tener inercia. En un medio inerte sus partículas constitutivas tienden a mantener un estado determiando y esto es lo que permite explicar, en última instancia el movimiento ondulatorio

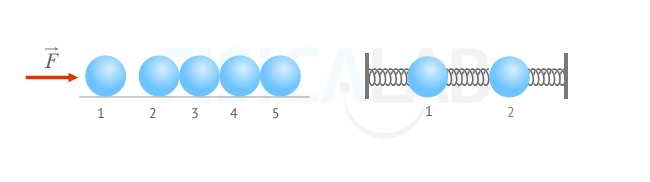
Propagación de ondas en medios elásticos

Cuando la bola 1 de la figura izquierda golpea la bola 2 se producirá una propagación de energía que hará que, al cabo de un tiempo, se desplace la bola 5. Esto se produce gracias a la elasticidad del medio. Si las bolas fuesen de plastilina la energía inicial de la bola se consumiría en su deformación y no llegaría a la última.

Por otro lado, observa que las bolas anteriores sólo propagarían el movimiento en una dirección y sentido. Si las uniésemos con muelles, como en la figura derecha, cualquiera que fuese la dirección del movimiento de la bola 1 sería transmitido a la bola 2.

Entonces, ¿en qué consiste exactamente la propagación? A medida que la onda avanza se produce una oscilación en torno al estado de equilibrio en alguna propiedad mecánica del medio. Puede ser la posición, la presión, la densidad o cualquier otra. Dicha fluctuación se extiende desde el foco emisor a los puntos colindantes. A continuación representamos esquemáticamente el proceso de propagación de una onda transversal en una cuerda tensa mediante lo que podrían ser partículas adyacentes de la misma.

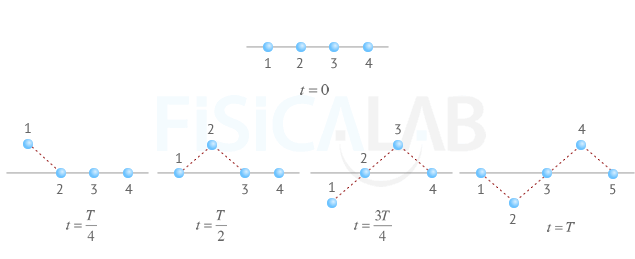
Esquema de propagación de onda mecánica en medio elástico

Cuando en un medio elástico provocamos una perturbación separándo el punto 1 de su posición de equilibrio, dicho punto inicia un movimiento vibratorio que, por la elasticidad del medio, se propaga al 2, posteriormente al 3 y así sucesivamente. Así se generaría una onda transversal. Cada uno de los puntos de la figura representa, esquematicamente, partículas adyacentes de una cuerda en tensión. El tiempo de oscilación de la partícula se denota por T

En general, los sólidos son capaces de propagar ondas mecánicas transversales y longitudinales y los fluidos sólo ondas longitudinales (salvo en su superficie, como la de un estanque, donde si se permite la aparición de transversales).

Velocidad de propagación

Cuando en una noche de tormenta entra un fogonazo de luz por tu ventana sabes que es muy probable que se deba a un rayo y que, pasados unos instantes, oirás el estruendo ocasionado por el mismo. Lo cierto es todas las ondas mecánicas, como el sonido, tienen una velocidad limitada de propagación.

Se puede comprobar que, en general, la velocidad de propagación puede expresarse en la forma:

$$v=\sqrt{\frac{propiedad elástica}{propiedad inercial}}$$

Así, aunque en general la obtención de la expresión de la velocidad de propagación para distintos medios y tipos de ondas queda fuera de los contenidos de este nivel, si que podemos señalar los siguientes casos particulares:

1. Velocidad de propagación de una onda transversal en una cuerda:

   $$v=\sqrt{\frac{T}{\mu }}$$

   Siendo T la tensión de la cuerda (propiedad elástica - [T]=N ) y μ la densidad lineal de masa de la cuerda (propiedad inercial - [μ]=kg/m )

2. Velocidad de propagación de una onda longitudinal en sólido:

   $$v=\sqrt{\frac{E}{\rho }}$$

   Siendo E el módulo de Young (propiedad elástica - [E]=kg·s^-2·m^-1) y ρ la densidad de masa del sólido (propiedad inercial - [ρ]=kg/m³)

3. Velocidad de propagación de ondas longitudinales en gases (sonido):

   $$v=\sqrt{\frac{\gamma ·R·T}{M}}$$

   Siendo en este caso T la temperatura ( [T]=K ), γ el coeficiente adiabático del gas (1.4 para el caso del aire), R la constante de los gases ideales ( R = 8.31 J·mol^-1·K^-1 ) y M la masa molecular del gas ( [M]= kg/mol ).

En todos los casos anteriores, y siempre que se utilicen las unidades indicadas, el resultado obtenido para v estará en metros por segundo (m/s). Finalmente, te invitamos a que realices el siguiente experimento sencillo que te permitirá comprobar la importancia del medio en la velocidad de propagación de la onda. Toma dos cuerdas de igual longitud y distinto peso. Para cada una de ellas, fija uno de los extremos a la pared y toma el otro con tu mano para generar un pulso. Comprueba que:

• Cuanto más tenses cada una de las cuerdas (propiedad elástica), más rápido avanza el pulso
• Cuanto más pesada es la cuerda (propiedad inercial), más lentamente avanza el pulso

Experimenta y Aprende

Cargando...

Velocidad de onda en cuerda

Las velocidad de las ondas depende de las características del medio. Pulsa sobre el botón play para comenzar a experimentar.

Ecuación de propagación

Llegados a este punto podemos describir matemáticamente el fenómeno de la propagación de una onda. Veamos.

La ecuación anterior simplemente pone de manifiesto que en la función de una onda deben aparecer combinados x y t en la forma x+v·t ó x-v·t. Recuerda que la función de una onda no es más que aquella expresión que sirve para describir matemáticamente la misma.

Comprobación

Vamos a buscar una expresión que nos permita describir matemáticamente la propagación de una onda. Para ello consideraremos un pulso único que se transmite de forma transversal a lo largo de una cuerda como la de la figura, a una velocidad v.

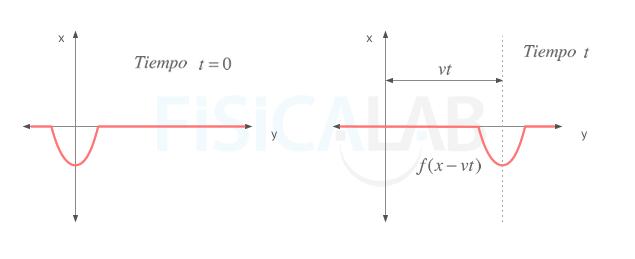
Ecuación de propagación

Cuando agitamos el extremo de una cuerda se genera un pulso que se propaga a velocidad uniforme. En la imagen se representa la forma de dicho pulso en dos instantes de tiempo diferentes t=0 y un instante genérico t. Observa que la forma del pulso es idéntica en los 2 casos, pero se produce un desplazamiento hacia la derecha a medida que avanza el tiempo equivalente al espacio recorrido por cualquier m.r.u.

Observa que en ambos instantes considerados tenemos la misma función pero desplazada una cierta distancia v·t. Dicho desplazamiento es fruto de la velocidad constante de la onda que determina que el espacio s recorrido por el pulso sea s=v·t. Por tanto, si de t=0 podemos concluir que y=f(x), de un instante genérico t podemos concluir que:

$$y=f\left(x-v·t\right)$$

Observa que la imagen anterior pone también de manifiesto que los valores concretos que toma la ondulación de la cuerda ( y ) en un determinado instante dependen de la posición x. Pero también se pone de manifiesto que fijando un determinado valor x, el correspondiente valor de y depende del instante de tiempo considerado.

Si repetimos el desarrollo para una onda que se desplaza hacia la izquierda, obtenemos:

$$y=f\left(x+s\right)=f\left(x+v·t\right)$$

Sintetizando las dos expresiones llegamos a la expresión que caracteriza las ondas mecánicas:

$$\boxed{y=f\left(x\pm v·t\right)}$$

Aunque en este desarrollo hemos considerado una onda que se propaga en una cuerda las conclusiones son válidas para cualquier onda que se desplace en la dirección del eje x.

¿Confundido con el significado de todo esto? Como siempre, el siguiente ejemplo te ayudará a aclararar las ideas...