Doble Periodicidad de la Función de Onda

En la Naturaleza se dan con frecuencia fenómenos que se repiten de forma exacta cada cierto tiempo. Son los fenómenos periódicos. Por ejemplo, el día y la noche fruto de la rotación de la Tierra sobre su eje, o las oscilaciones de un péndulo simple, si despreciamos la resistencia del aire, se pueden considerar fenómenos periódicos. Existe también otro tipo de periodicidad que tiene que ver con el espacio y no con el tiempo. Por ejemplo, si observas los mosaicos de la Alhambra de Granada, te darás cuenta que se repiten de manera exacta cada cierta distancia.

Mosaico de la Alhambra de Granada

Muchos mosaicos árabes son un ejemplo claro de periodicidad espacial. En ellos, un motivo mínimo se repite a lo largo y ancho de la extensión que ocupan.

En este apartado vamos a comprobar, a partir de su ecuación, que las ondas armónicas cumplen los dos tipos de periodicidad: temporal y espacial, es decir, son doblemente periódicas.

Recuerda que la ecuación de una onda armónica que se propaga en una sola dimensión viene dada, en una de sus múltiples formas, por la expresión:

$$y\left(x,t\right)=A·\sin \left(2·\pi ·\left(\frac{t}{T}-\frac{x}{\lambda }\right)\right)$$

Periodicidad temporal

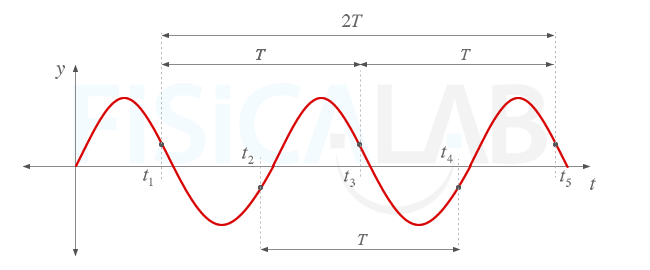
Onda respecto al tiempo

Si representamos en el eje de abcisas el tiempo y en el eje de ordenadas la elongación de una partícula cualquiera vemos que cualquier elongación se repite cada cierto periodo T y a múltiplos del mismo.

Para comprobar la periodicidad respecto al tiempo de la función de onda estudiaremos la elongación y de una partícula concreta de la onda situada a una distancia fija x del origen en dos instantes de tiempo distintos, t y  t+n·T, siendo n cualquier número entero ( n ∈ Z ). Nos queda:

$$\begin{gathered} t\Rightarrow y\left(x,t\right)=A·\sin \left(2·\pi ·\left(\frac{t}{T}-\frac{x}{\lambda }\right)\right); \\ t+n·T\Rightarrow y\left(x,t+n·T\right)=A·\sin \left(2·\pi ·\left(\frac{t+n·T}{T}-\frac{x}{\lambda }\right)\right); \end{gathered}$$

Ahora bien, sabemos que $\sin \left(a\right)=\sin \left(a+2·\mathrm{\pi }·\mathrm{n}\right)$ , por lo que podemos escribir:

$$y\left(x,t+n·T\right)=A·\sin \left(2·\pi ·\left(\frac{t+n·T}{T}-\frac{x}{\lambda }\right)\right)=A·\sin \left(2·\pi ·\left(\frac{t}{T}-\frac{x}{\lambda }\right)+2·\pi ·n\right)=A·\sin \left(2·\pi ·\left(\frac{t}{T}-\frac{x}{\lambda }\right)\right)=y\left(x,t\right)$$

Que es justamente lo que queríamos comprobar.

Periodicidad espacial

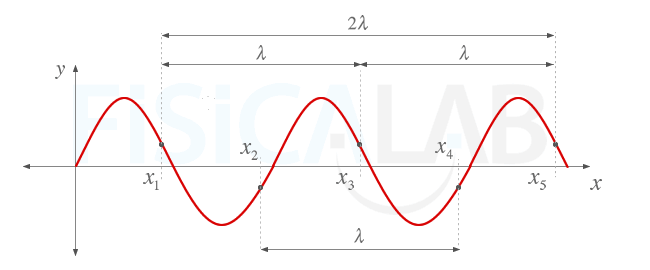
Onda respecto al espacio

Si representamos en el eje de abscisas la distancia de las partículas respecto al origen y en el eje de ordenadas la elongación de las partículas en un instante concreto cualquiera vemos que cualquier valor de elongación se repite cada cierta distancia λ y a múltiplos de la misma.

Para comprobar la periodicidad respecto al espacio (o la posición) de la función de onda consideramos un instante t fijo y estudiaremos la elongación y de dos partículas distintas, una situada en x y otra en x+n·λ, siendo n cualquier número entero ( n ∈ Z ). Nos queda:

$$\begin{gathered} x\Rightarrow y\left(x,t\right)=A·\sin \left(2·\pi ·\left(\frac{t}{T}-\frac{x}{\lambda }\right)\right); \\ x+n·\lambda \Rightarrow y\left(x+n·\lambda ,t\right)=A·\sin \left(2·\pi ·\left(\frac{t}{T}-\frac{x+n·\lambda }{\lambda }\right)\right); \end{gathered}$$

Ahora bien, sabemos que $\sin \left(a\right)=\sin \left(a-2·\mathrm{\pi }·\mathrm{n}\right)$ , por lo que podemos escribir:

$$y\left(x+n·\lambda ,t\right)=A·\sin \left(2·\pi ·\left(\frac{t}{T}-\frac{x+n·\lambda }{\lambda }\right)\right)=A·\sin \left(2·\pi ·\left(\frac{t}{T}-\frac{x}{\lambda }\right)-2·\pi ·n\right)=A·\sin \left(2·\pi ·\left(\frac{t}{T}-\frac{x}{\lambda }\right)\right)=y\left(x,t\right)$$

Que es justamente lo que queríamos comprobar.