Puntos de Inflexión y Curvatura de una Función

Estudiar la curvatura de una función consiste en determinar aquellos intervalos en los que la función es cóncava, y en cuáles es convexa. En aquellos puntos en los que la función pasa de un tipo de curvatura a otro, decimos que hay un punto de inflexión.

Curvatura de una función

En el apartado de análisis de funciones ya hicimos una primera aproximación a los conceptos de concavidad y convexidad en un intervalo. Observa:

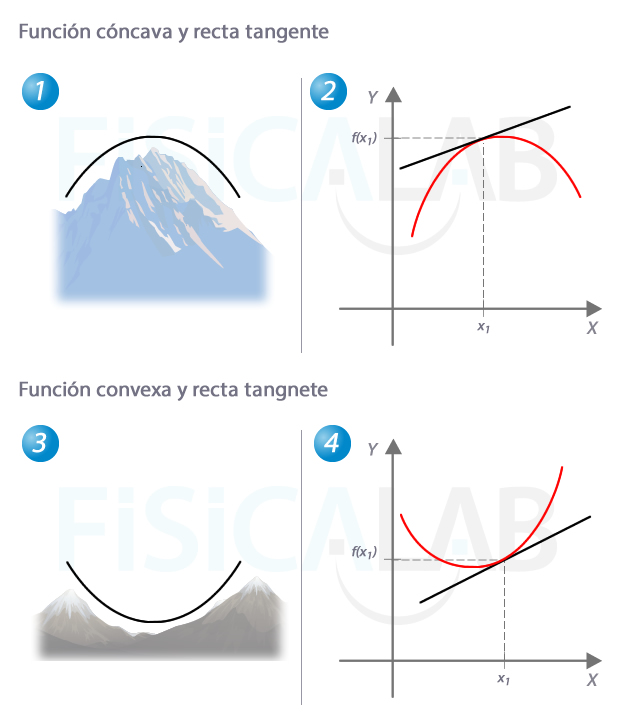
Podemos visualizar un tramo cóncavo de una función como una montaña, tal y como se ve en 1. En 2 vemos que la recta tangente en un punto en el que la función es cóncava siempre queda por encima de la propia función.

Por otro lado, para visualizar un tramo convexo, podemos utilizar el símil de un valle entre montañas, como la de 3. En 4 observamos que la recta tangente en un punto en el que la función es convexa siempre queda por debajo de la propia función.

En este apartado vamos a darte las herramientas matemáticas para poder hacer un estudio sistemático de la curvatura, y de los puntos de inflexión. Vamos a estudiar:

• Los criterios de concavidad y convexidad
• Los puntos de inflexión
• Las implicaciones de la curvatura en el cálculo de los máximos y de los mínimos
• La regla práctica para el estudio de la curvatura y los puntos de inflexión

¡Vamos con ello!

Criterios de concavidad y convexidad

Para entender de dónde vinen estas expresiones, observa las características geométricas de las funciones cónvavas y convexas en la siguientes imágenes:

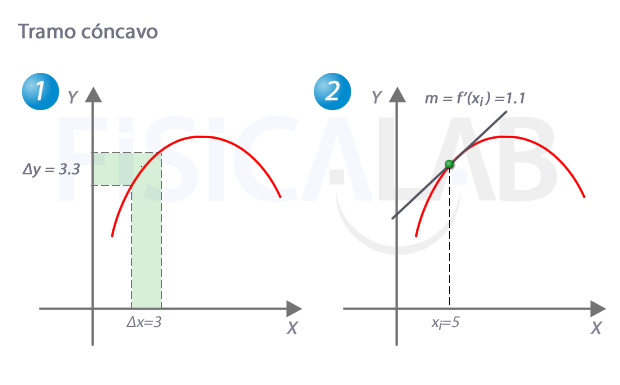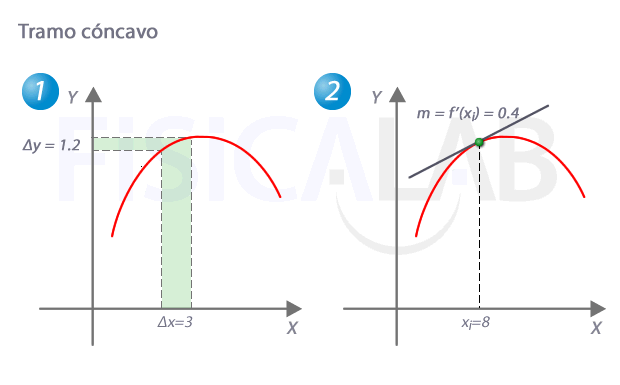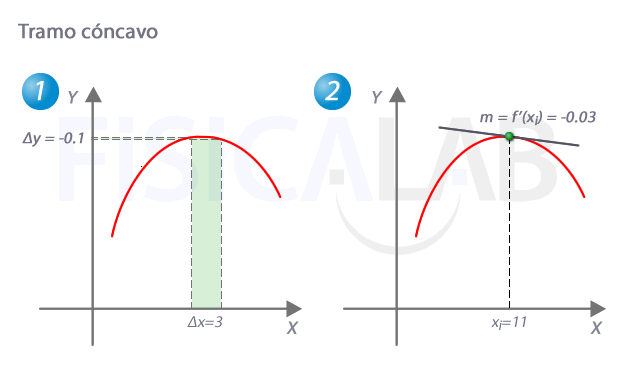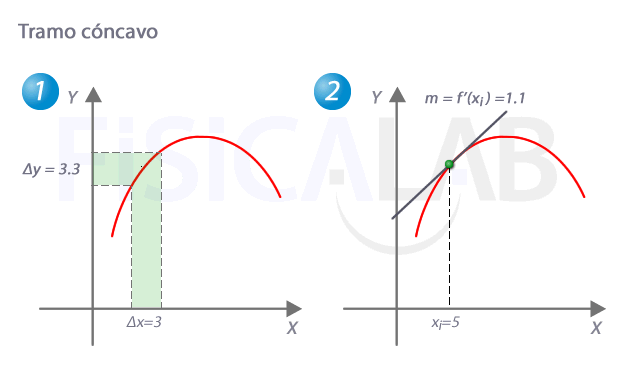
Tramo cóncavo

En un tramo cóncavo de una función, como el que hay en 1, para incrementos de x equiespaciados (Δx), los incrementos de y (Δy) son cada vez menores. Esto implica, tal y como se ve en 2, que la pendiente de la recta tangente va decreciendo a medida que aumentamos la x.

¿Qué significa que la pendiente de la recta tangente vaya decreciendo? Ni más ni menos que la primera derivada es decreciente en todos los puntos de ese tramo (recuerda que la primera derivada es la que tiene el valor de la pendiente de la recta tangnete a la función original en cada punto). En las funciones decrecientes, la derivada es menor que cero, con lo que podríamos escribir:

$$\left(f\text{'}\right)\text{'}<0\iff f\text{'}\text{'}<0$$

Por otro lado...

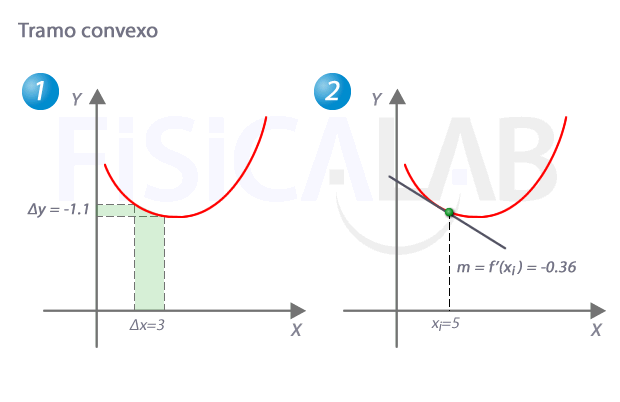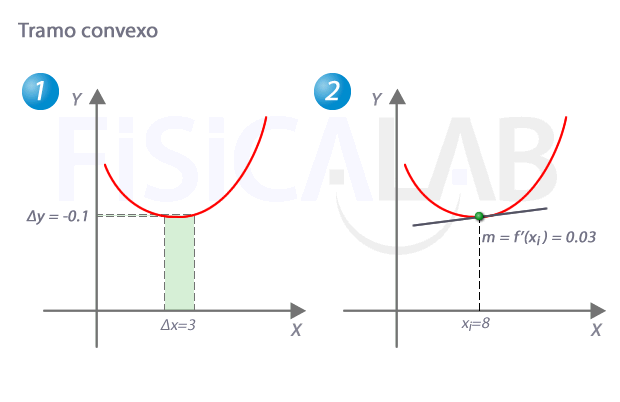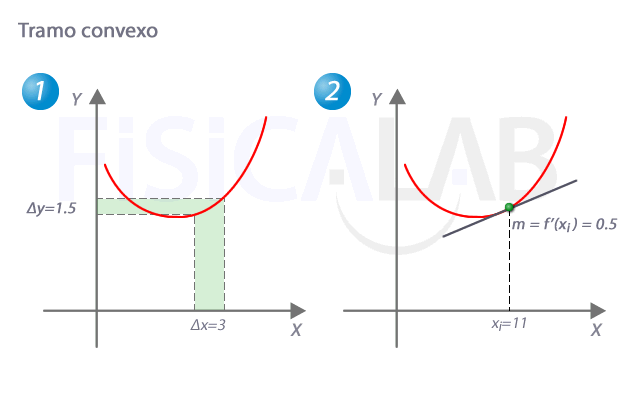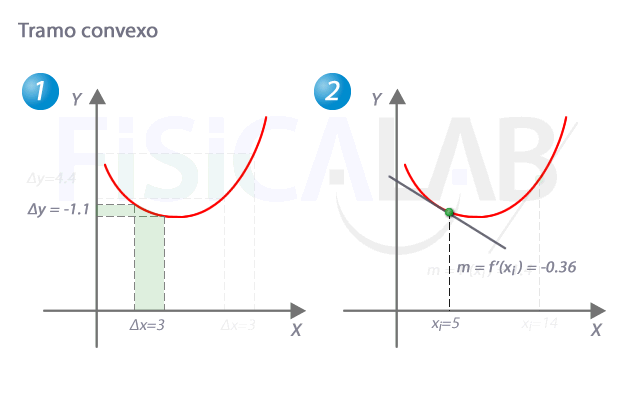
Tramo convexo

En un tramo convexo de una función, como el que hay en 1, para incrementos de x equiespaciados (Δx), los incrementos de y (Δy) son cada vez mayores. Esto implica, tal y como se ven en 2, que la pendiente de la recta tangente va creciendo a medida que aumentamos la x.

¿Qué significa que la pendiente de la recta tangente vaya creciendo? Ni más ni menos que la primera derivada es creciente en todos los puntos de ese tramo (de nuevo, recuerda que la primera derivada es la que tiene el valor de la pendiente de la recta tangnete a la función original en cada punto). En las funciones crecientes, la derivada es mayor que cero, con lo que podríamos escribir:

$$\left(f\text{'}\right)\text{'}>0\iff f\text{'}\text{'}>0$$

Puntos de inflexión

Los puntos de inflexión son aquellos en los que la función pasa de cóncava a convexa o de convexa a cóncava. Matemáticamente esto ocurre cuando la segunda derivada de la función en el punto considerado cambia de signo, y además la función f está definida en el punto considerado.

Punto de inflexión

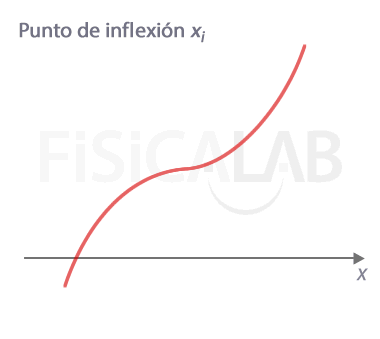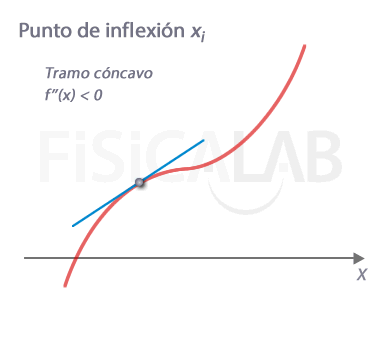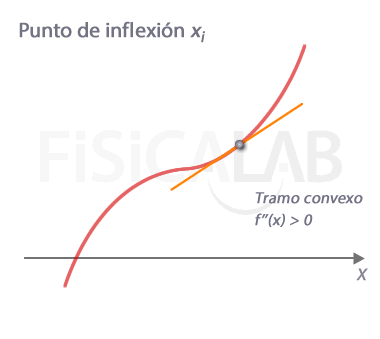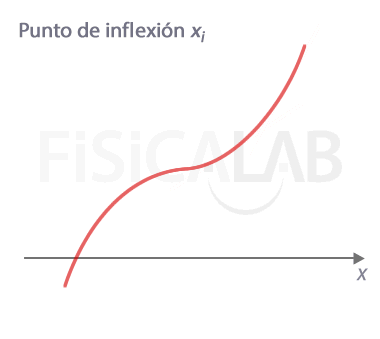
En x=x_i tenemos un punto en el que cambia la curvatura de la función. Es por tanto un punto de infléxión. Observa que en él la recta tangente queda por encima de la función en un lado, y por debajo en otro, es decir, la "atraviesa". Además, el signo de la segunda derivada es diferente a la izquierda y a la derecha del punto, siendo f''(x_i)=0.

¿Por qué f''(x_i)=0?

Como hemos indicado, partimos de la premisa de que la segunda derivada es continua en x_i. Para que haya un cambio de curvatura se debe cumplir que en cualquier entorno de x_i la segunda derivada tenga signos distintos. Debido a la continuidad de f'' esto implica necesariamente que en el propio punto debe ser 0, es decir, f''(x_i)=0.

Esta condición, aunque necesaria, no es suficiente, de ahí que también sea necesario que f'''(x_i)≠0

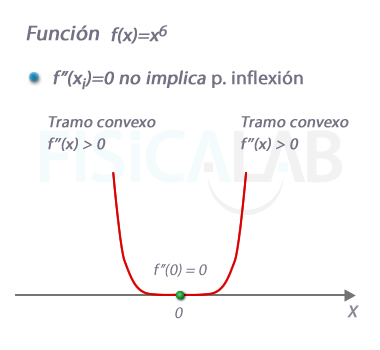
Punto de inflexión y segunda derivada

La función f(x)=x⁶ representada en la figura cumple que f''(0)=0, sin embargo puedes ver que en x=0 no cambia su curvatura (que es la misma en todo su dominio). Así, el signo de f'' es el mismo en ambos lados de 0.

¿Por qué f'''(x_i)≠0?

Esta condición asegura que el signo de f''(x) sea diferente a ambos lados de un punto de inflexión x_i. ¿Por qué? El signo de f'' será diferente cuando f'' crezca o decrezca en x_i, es decir, cuando su primera derivada (f''') sea positiva (creciente) o negativa (decreciente). En cualquier caso cuando f'''(x_i)≠0.

Implicaciones en la identificación de máximos y mínimos

Intuitivamente puedes observar que en un tramo cóncavo de una función (con forma de montaña), si la pendiente de la recta tangente (f'(x)) se hace 0, se trata de un máximo. Análogamente, en un tramo convexo (con forma de valle), si la pndiente de la rcta tangente (f'(x)) se hace 0, se trata de un mínimo.

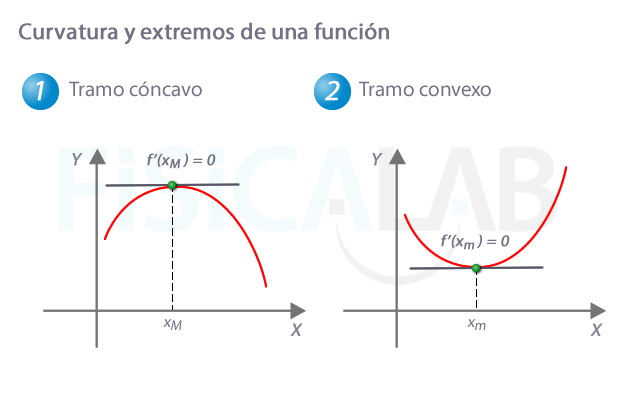
Curvatura y extremos de una función

En una función cóncava, como la que hay en 1, los valores que anulan la primera derivada son máximos relativos (que podrían ser absolutos si no existe ninguna imagen de f mayor). En una convexa, como la que hay en 2, los valores que anulan la primera derivada son mínimos relativos (que también podrían ser absolutos si no existe ninguna imagen de f menor).

Matemáticamente...

Demostración

Demostraremos aquí que si f'(x_i)=0 y f''(x_i)<0, entonces la función tiene un máximo relativo en x_i. La demostración para el mínimo es análoga y la dejamos como ejercicio propuesto.

De la definición de deivada de una función, aplicada a f''(x_i), tenemos que...

$$f\text{'}\text{'}\left(x_i\right)=\underset{h\to 0}{\lim }\frac{f\text{'}\left(x_i+h\right)-f\text{'}\left(x_i\right)}{h}\underset{f\text{'}\left(x_i\right)=0}{=}\underset{h\to 0}{\lim }\frac{f\text{'}\left(x_i+h\right)}{h}<0$$

Ahora...

1. Si h<0, como , $\underset{h\to 0}{\lim }\frac{f\text{'}\left(x_i+h\right)}{h}<0$, entonces f'(x_i+h)>0, con lo que f es creciente a la izquierda (h<0) de x_i
2. Si h>0, como , $\underset{h\to 0}{\lim }\frac{f\text{'}\left(x_i+h\right)}{h}<0$, entonces f'(x_i+h)<0, con lo que f es decreciente a la derecha (h>0) de x_i

Las dos condiciones anteriores implican que x_i es un máximo relativo.

Regla práctica

Aplicando los criterios prácticos presentados hasta ahora, debería ser inmediato saber si una función es cóncava, convexa o presenta un punto de inflexión en un punto dado. La dificultad estriba en saber obtener sus intervalos de concavidad, convexidad, y los puntos de inflexión cuando te proporcionan únicamente la función. Te recomendamos que sigas los siguientes pasos:

1. Determinar el dominio de la función, para asegurarnos que los puntos que vamos a obtener pertenecen al mismo

2. Determina la expresión de la segunda derivada de la función

3. Obtén los candidatos a puntos de inflexión de la función a partir de su segunda derivada:

   • Los puntos que hacen f''(x)=0

   • Los puntos en los que ∄ f''(x) (aunque en este nivel educativo no será frecuente que veas ejercicios con este caso)

4. Estudia el signo de f'' ayudándote de un cuadro de signos. Coloca en dicho cuadro, sobre el dominio de la función, los candidatos a puntos de inflexión obtenidos, y en cada intervalo resultante determina el signo de la segunda derivada

5. En los intervalos de signo negativo, la función original es cóncava. En los intervalos de signo positivo, la función es convexa

6. Aquellos candidatos a puntos de inflexión en los que se produzca un cambio de curvatura son, efectivamente, puntos de inflexión

Te recomendamos que realices los ejercicios asociados a este apartado para poder asimilar estas ideas. ¡Verás que es muy sencillo!