Análisis de Funciones

El análisis de funciones consiste en el estudio de las características de las mismas a fin de poder describir con precisión los fenómenos que representan. Por ejemplo, si tenemos una función que describe la evolución de la temperatura de un determinado objeto a medida que le suministramos calor, conociendo su máximo y su mínimo podremos saber el rango de temperaturas para el cual estar preparados cuando manipulemos el objeto en cuestión. El estudio de una función comprende principalmente los siguientes elementos:

Dominio
Recorrido
Ceros
Signo
Monotonía
- Crecimiento y decrecimiento
- Máximos y mínimos
Curvatura
Acotación (supremos e ínfimos)
Simetría
Periodicidad

¿Empezamos?

Dominio

Como ya sabes, el dominio de una función es el conjunto de valores para los cuales está definida. Ya hemos visto que se puede restringir el dominio de una función real por distintas razones:

Cuando sea matemáticamente imposible realizar alguna operación con ciertos valores x. Por ejemplo, en la función f(x)=1/x, el valor de x puede ser cualquiera salvo x=0, ya que ningún número se puede dividir entre cero. De ahí que Dom_f=ℝ-{0}
Cuando el contexto real del que se ha obtenido la función así lo determine. Por ejemplo, en el caso del valor de la fuerza gravitatoria con que se atraen dos partículas, la fuerza puede ser considerada como una función que depende de la distancia entre las mismas, y no tiene sentido que esta sea negativa
Cuando lo necesitemos por alguna otra razón

Es habitual empezar el análisis de una función estudiando su dominio. Recuerda:

Para calcular el dominio:

Si tenemos la expresión analítica de una función (su ecuación), determinamos su dominio buscando los valores de x para los que no está definida y quitándolos de ℝ
Si lo que tenemos es la gráfica de la función, el dominio se calcula proyectando la función sobre el eje horizontal x

Recorrido

El recorrido de una función es el conjunto de valores que toma la función. Ya hemos visto en un apartado anterior como calcularlo. Recuerda:

Para calcular el conjunto imagen o recorrido de la función:

Si tenemos la expresión analítica de la función, y esta tiene inversa, el dominio de esta última es el recorrido de la función original
Si lo que tenemos es la gráfica de la función, o podemos esbozarla, determinamos el recorrido proyectando sobre el eje y

Ceros

Los ceros de una función son los puntos de corte con el eje horizontal x. Todos cumplen que f(x)=y=0. Son importantes porque en ellos la función puede cambiar de signo.

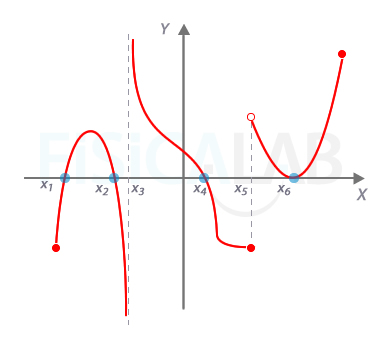
Ceros de la función

La gráfica de la figura representa una función con tres secciones o ramas. En azul se han señalado los ceros de la misma. La rama más a la izquierda cuanta con dos ceros, en x=x₁ y x=x₂. En la segunda rama, hay un cero, en x=x₄. En la tercera rama hay un cero en x=x₆.

Observa que en x=x₁ la función pasa de ser negativa a ser positiva; en x=x₂ y x=x₄ pasa de ser positiva a ser negativa; En x=x₆ no cambia el signo. Por otro lado, observa que en la asíntota vertical x=x₃ y en el cambio de rama x=x₅, la función pasa de negativa a positiva sin que haya ningún cero.

Para calcular los ceros:

Si tenemos la expresión analítica de una función (su ecuación), resolvemos f(x)=0
Si lo que tenemos es la gráfica de la función, los ceros son los puntos de corte de la gráfica con el eje x

Signo

Estudiar el signo de una función consiste en determinar el conjunto de valores de x para los cuales f(x)>0, (signo positivo) y el conjunto de valores para los cuales f(x)<0, (signo negativo).

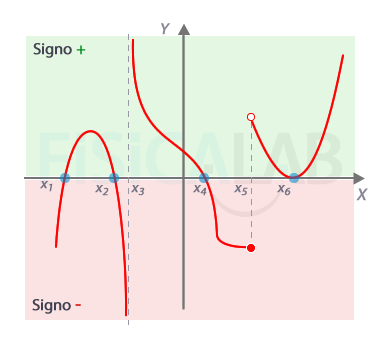
Signo de una función

En la ilustración tenemos, en trazo rojo, la gráfica de una función. Los tramos en los que transcurre por encima del eje x (y>0), son tramos de signo positivo. Estos son: (x₁, x₂), (x₃, x₄) y (x₆, ∞). Los tramos en los que transcurre por debajo del eje x (y<0) son tramos de signo negativo. Estos son: (-∞, x₁), (x₂, x₃) y (x₄, x₅).

Para calcular los intervalos de signo constante:

Si tenemos la expresión analítica buscamos los valores de x en los que la función puede cambiar de signo. Estos son:
- Los ceros de la función
- Las asíntotas verticales (en el caso de las funciones racionales, por ejemplo, los puntos que anulan el denominador)
- Los cambios de rama
Éstos valores de x dividen la recta real en varios intervalos. Para averiguar el signo de la función en cada uno de ellos, se elige un valor de x al azar de cada intervalo (x_i) y se calcula su imagen (f(x_i)). El signo de f(x_i) será el signo de la función en ese intervalo.
Si lo que tenemos es la gráfica de la función, los intervalos de signo positivo son aquellos en los que la función queda por encima del eje x, y los de signo negativo, aquellos en los que queda por debajo

Normalmente nos valdremos de un cuadro de signos para determinar los intervalos de signos constantes en las funciones cuando estas se puedan factorizar. El siguiente ejemplo te aclarará estos procedimientos.

Ejemplo

Estudia los intervalos de signo constante en las siguientes funciones:

$f (x) = - \frac{1}{2} x^{2} + \frac{1}{2} x + 3$
$f (x) = \frac{x + 2}{x - 2}$
$f (x) = \frac{x^{2}}{x + 4}$
$f (x) = x - \frac{9}{x}$

Ver solución

Monotonía

Estudiar la monotonía de una función consiste en estudiar su crecimiento y su decrecimiento, sus máximos y sus mínimos. En este punto vamos a introducir todos estos conceptos, y a darte una primera aproximación sobre como puedes trabajarlos. En apartados posteriores te enseñaremos a hacerlo de manera más sistematizada, mediante derivadas.

Crecimiento y decrecimiento

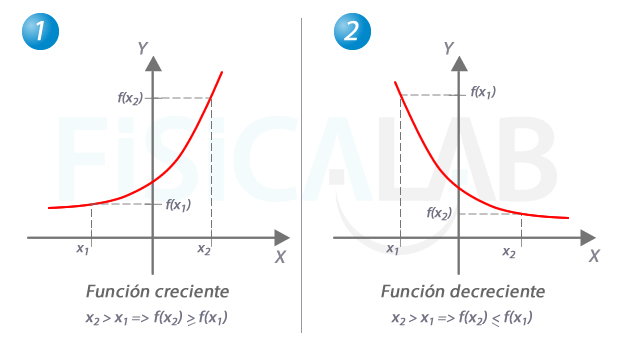
Idea intuitiva de crecimiento

A la izquierda, en 1, un tramo creciente de una función. A medida que aumenta el valor de x aumenta también el valor de y correspondiente. A la derecha, en 2, un tramo decreciente de una función. A medida que aumenta el valor de x, disminuye el valor de y correspondiente.

A la vista de estas ideas intuitivas podemos hacer las siguientes definiciones.

Decimos que una función f(x) es creciente en un intervalo (l_i, l_s) de su dominio si para cualquier par de valores x₁, x₂ pertenecientes a dicho intervalo y con x₂>x₁, se cumple que f(x₂)≥f(x₁). Si además se cumple que f(x₂)>f(x₁) decimos que la función es estrictamente creciente en ese intervalo.

Decimos que una función es creciente (a secas) cuando lo es en todo su dominio. Igualmente, decimos que una función es estrictamente creciente (a secas) cuando lo es en todo su dominio.

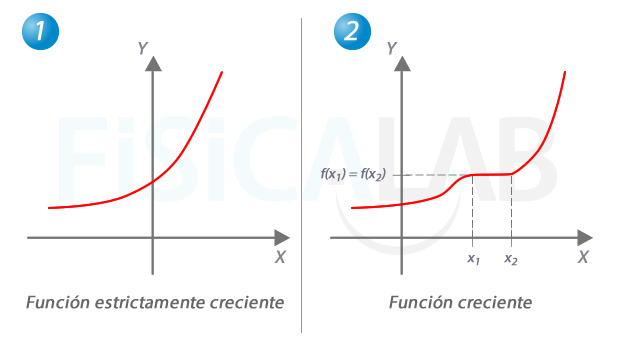
Función estrictamente creciente vs función creciente

A la izquierda, en 1, una función estrictamente creciente. A la derecha, en 2, una función creciente. En esta última puede haber dos valores de x con igual imagen, como es el caso de x₁ y x₂.

Decimos que una función f(x) es decreciente en un intervalo (l_i, l_s) de su dominio si para cualquier par de valores x₁, x₂ pertenecientes a dicho intervalo y con x₂>x₁, se cumple que f(x₂)≤f(x₁). Si además se cumple que f(x₂<f(x₁) decimos que la función es estrictamente decreciente en ese intervalo.

Decimos que una función es decreciente (a secas) cuando lo es en todo su dominio. Igualmente, decimos que una función es estrictamente decreciente (a secas) cuando lo es en todo su dominio.

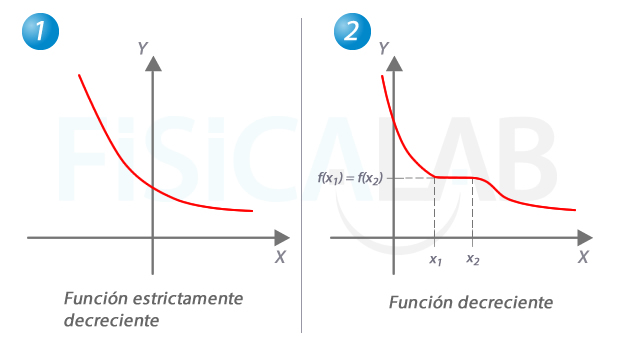
Función estrictamente decreciente vs función decreciente

A la izquierda, en 1, una función estrictamente decreciente. A la derecha, en 2, una función decreciente. En esta última puede haber dos valores de x con igual imagen, como es el caso de x₁ y x₂.

Observa que una función no necesariamente tiene que ser creciente o decreciente en todo su dominio, sino que puede tener intervalos de crecimiento e intervalos de decrecimiento. Además recuerda que una función también puede ser constante cuando cumple f(x)=k.

Criterio de la recta tangente

La recta tangente a la función es creciente en los intervalos de crecimiento (pendiente positiva m>0) y decreciente (pendiente negativa m<0) en los de decrecimiento. Este criterio supone la base para sistematizar el estudio de la monotonía de las funciones, y, como te hemos dicho, volveremos a él cuando conozcas las derivadas.

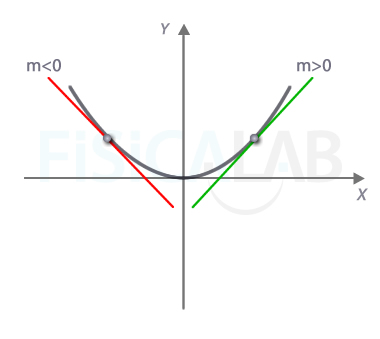
Crecimiento y recta tangente

Podemos averiguar si estamos en un intervalo de crecimiento o de decrecimiento estudiando la pendiente de la recta tangente. A la izquierda, en el intervalo de decrecimiento de la parábola negra, la recta, en rojo, está orientada hacia abajo (pendiente negativa). A la derecha, en el intervalo de crecimiento, la recta, en verde, está orientada hacia arriba (pendiente positiva).

Máximos y mínimos

A los máximos y mínimos se les denomina de manera genérica extremos de la función y pueden ser absolutos o relativos.

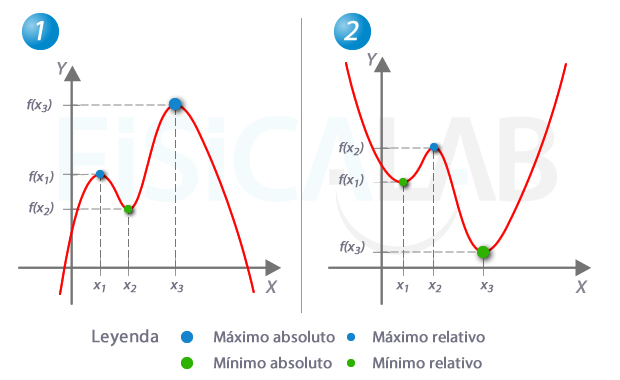
Idea intuitiva de extremos

Observando las dos gráficas de la ilustración resulta inmediato identificar intuitivamente los máximos y los mínimos. Los máximos son los puntos más grandes de la función en su entorno. Los mínimos son los más pequeños. Dado un máximo, cuando el valor de su coordenada y es superior o igual al resto de imágenes de la función, se trata de un máximo absoluto. Si no, es un máximo relativo. Análogamente, dado un mínimo, cuando el valor de su coordenada y es inferior o igual al resto de imágenes de la función, se trata de un mínimo absoluto. Si no, es un mínimo relativo.

A partir de esta idea intuitiva, veamos dónde pueden encontrarse.

Cuando una función pasa de creciente a decreciente la función tiene un extremo llamado máximo. Cuando pasa de decreciente a creciente la función tine un extremo llamado mínimo. Estos extremos pueden ser locales (relativos) o globales (absolutos).

Un máximo es absoluto cuando la función nunca supera el valor del máximo en ningún otro punto de su dominio. Por tanto, una función puede tener varios máximos absolutos, pero su valor en ellos debe ser único. Si no es absoluto, el máximo es relativo. Análogamente, un mínimo es absoluto cuando la función nunca iguala ni queda por debajo de la imagen del mínimo en todo su dominio. Igualmente, pueden existir varios mínimos absolutos, pero el valor de todos ellos será el mismo. Si no es absoluto, el mínimo es relativo

Los extremos de la función pueden aparecer, además, en los extremos del dominio o en los puntos de cambio de rama en el caso de las funciones definidas a trozos.

Máximos y mínimos absolutos y relativos en función con dominio acotado y en funciones a trozos

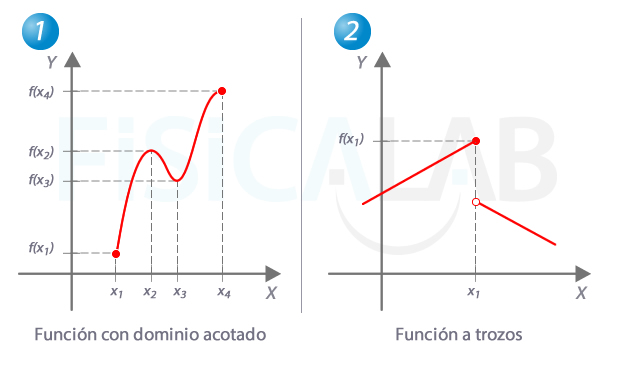
Extremos en funciones con dominio acotado y funciones a trozos

A la izquierda, una función con un dominio acotado al intervalo [x₁, x₄]. El mínimo absoluto, en este caso, se encuentra precisamente en uno de los extremos del dominio de definición (x₁,f(x₁)). El máximo absoluto en el otro extremo ((x₄,f(x₄))). Por otro lado, los puntos en los que la función pasa de creciente a decreciente (x₂,f(x₂)) y de decreciente a crecinte (x₃,f(x₃)) son en este caso extremos relativos (máximo y mínimo respectivamente).

En la función derecha el máximo absoluto se produce en un cambio de rama (x₁,f(x₁)).

Ten presente que algunos textos no consideran la posibilidad de que un máximo o un mínimo aparezca en los extremos del dominio.

Por otro lado, y de manera general, para encontrar los máximos y los mínimos de una función hay que calcular sus puntos críticos. No tengas prisa, te enseñaremos a hacerlo cuando te hayamos presentado las derivadas, en el apartado dedicado específicamente a extremos de la función, pero, ¿sabrías decir ya qué pasa en los máximos y los mínimos con la recta tangente?

De manera particular, la parábola vertical es un ejemplo sencillo en el que puedes calcular sus máximos o mínimos absolutos, así como sus intervalos de crecimiento y de decrecimiento. Recuerda que el vértice de la misma constituía el mínimo absoluto de la función si esta tenía las ramas hacia arriba (a>0), o el máximo absoluto si tenía las ramas hacia abajo (a<0). La siguiente tabla recoge estas ideas:

*Expresión general* f(x)=a·x²+b·x+c	*Mínimo*	*Máximo*	*Decrecimiento*	*Crecimiento*
a>0	Vértice $(\frac{- b}{2 a}, f (\frac{- b}{2 a}))$	∄	(-∞, x_v)	(x_v, ∞)
a<0	∄	Vértice $(\frac{- b}{2 a}, f (\frac{- b}{2 a}))$	(x_v, ∞)	(-∞, x_v)

Curvatura

Estudiar la curvatura de una función consiste en estudiar su concavidad y su convexidad, así como sus puntos de inflexión. En este punto vamos a introducir todos estos conceptos, y a darte una primera aproximación sobre como puedes trabajarlos. Al igual que con la monotonía, en apartados posteriores te enseñaremos a estudiar la curvatura mediante derivadas.

Concavidad

Decimos que una función es cóncava en un intervalo cuando el segmento que une dos puntos cualesquiera del intervalo siempre queda debajo de la gráfica. A las funciones cóncavas también se las llama cóncavas hacia abajo. Matemáticamente, una función es cóncava en un intervalo (x₁, x₂) cuando cualquier valor x∈(x₁, x₂) se cumple:

\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} \leq \frac{f (x) - f (x_{1})}{x - x_{1}}

Decimos que una función es cóncava cuando lo es en todo su dominio.

Características geométricas de las funciones cóncavas

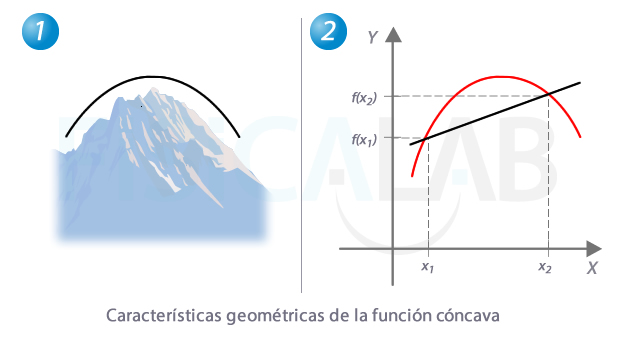
Función cóncava

Para visualizar una función cóncava puedes imaginar una montaña como la de la izquierda. A la derecha, en negro, un segmento trazado entre dos puntos cualesquiera entre x₁ y x₂ siempre quedará por debajo de un tramo cóncavo.

Observa que en el entorno de un máximo, la función que pasa de creciente a decreciente es cóncava.

Convexidad

Decimos que una función es convexa en un intervalo cuando el segmento que une dos puntos cualesquiera del intervalo siempre queda encima de la gráfica. A las funciones convexas también se las llama cóncavas hacia arriba. Matemáticamente, una función es cóncava en un intervalo (x₁, x₂) cuando cualquier valor x∈(x₁, x₂) se cumple:

\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} \geq \frac{f (x) - f (x_{1})}{x - x_{1}}

Decimos que una función es convexa cuando lo es en todo su dominio.

Características geométricas de las funciones convexas

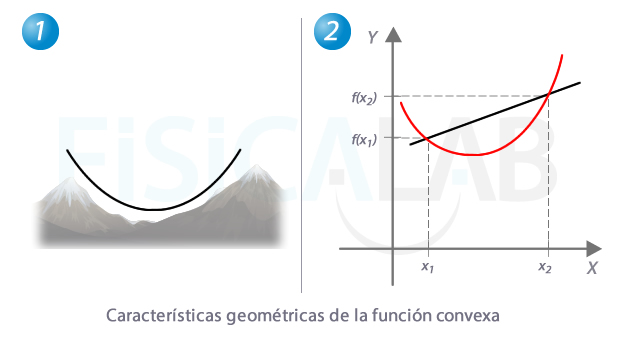
Función convexa

Para visualizar una función convexa, en este caso, utilizaremos el símil de un valle entre montañas como la de la izquierda. A la derecha, en negro, un segmento trazado entre dos puntos cualesquiera entre x₁ y x₂ siempre quedará por encima de un tramo convexo.

Observa que en el entorno de un mínimo, la función que pasa de decreciente a creciente es convexa.

En ocasiones puedes encontrar textos en los que los criterios de concavidad y convexidad sean justo los contrarios a los que te hemos presentado aquí.

Criterio de la recta tangente

La recta tangente a la función queda siempre por encima de esta en las funciones cóncavas y por debajo en las funciones convexas. Este criterio de puede ayudar a identificar los intervalos de concavidad y convexidad en las gráficas de funciones.

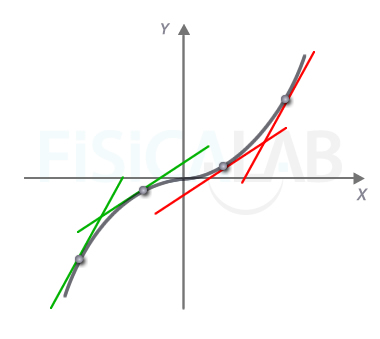
Curvatura y recta tangente

Podemos averiguar si estamos en un intervalo cóncavo o convexo "imaginando" como sería la recta tangente en cualquiera de sus puntos. A la izquierda, en el intervalo cóncavo, las rectas tangentes, en verde, quedan encima de la función, en negro, en cualquier punto. A la derecha, en el intervalo convexo, las rectas tangentes, en rojo, quedarían por debajo de la curva.

Puntos de inflexión

Una función tiene un punto de inflexión cuando cambia su curvatura, es decir, cuando pasa de cóncava a convexa o de convexa a cóncava. En un punto de inflexión la recta tangente queda por encima de la función en un lado, y por debajo en otro, es decir, la "atraviesa".

Acotación

De manera intuitiva, podemos decir que una función está acotada por arriba cuando el valor de sus imágenes nunca supera un determinado valor constante. Análogamente, podemos decir que una función está acotada por abajo cuando el valor de sus imágenes nunca es inferior a un determinado valor constante. Veamos unas definiciones un poco más formales.

Una función está acotada superiormente si existe un número real k tal que f(x)≤k para cualquier valor de x∈Dom_f. Al valor y=k se le llama cota superior de la función.

Función acotada superiormente y cotas superiores

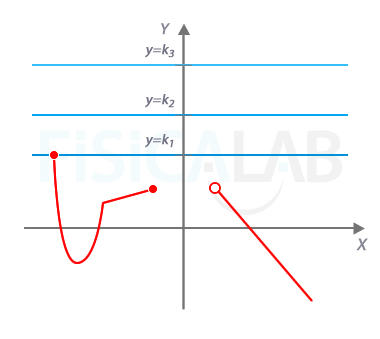
Cotas superiores y supremo

La gráfica de la figura representa una función cuyo valor máximo es k₁. Se trata, por tanto, de una función acotada superiormente. Todas las funciones acotadas superiormente tienen infinitas cotas superiores (por ejemplo, y=k₁, y=k₂ o y=k₃). A la menor de las cotas superiores se le llama supremo. k₁ es el supremo de la función de nuestro ejemplo.

Una función está acotada inferiormente si existe un número real k tal que f(x)≥k para cualquier valor de x∈Dom_f. Al valor y=k se le llama cota inferior de la función.

Función acotada inferiormente y cotas inferiores

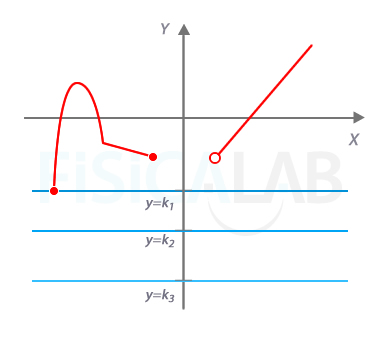
Cotas inferiores e ínfimo

La gráfica de la figura representa una función cuyo valor mínimo es k₁. Se trata, por tanto, de una función acotada inferiormente. Todas las funciones acotadas inferiormente tienen infinitas cotas inferiores (por ejemplo, y=k₁, y=k₂, y=k₃). A la mayor de las cotas inferiores se le llama ínfimo. k₁ es el ínfimo de la función de nuestro ejemplo.

Cuando una función está acotada superior e inferiormente podemos decir que la función está acotada (a secas).

Una función está acotada si existe un número real k tal que |f(x)|≤k para cualquier valor de x∈Dom_f. El valor y=k será una cota superior de la función, e y=-k una cota inferior, aunque no necesariamente serán el supremo y el ínfimo respectivamente.

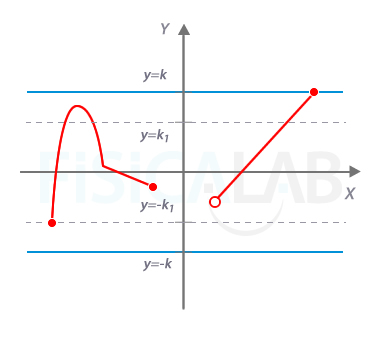
Función acotada

La gráfica de la figura representa una función. Efectivamente, se cumple que -k≤f(x)≤k, con lo que se trata de una función acotada. Observa que y=k es el supremo de la función, cuyo opuesto, y=-k,no es el ínfimo (aunque sí una cota inferior). El ínfimo es y=-k₁, cuyo opuesto y=k₁, sin embargo, no es siquiera cota superior de f(x).

Finalmente, observa que cuando una función está acotada, los extremos de su recorrido son necesariamente valores finitos.

Para calcular si una función está acotada, calculamos su recorrido:

Si el extremo superior es un valor finito, la función está acotada superiormente. Si, además, la función alcanza su supremo en uno o varios puntos, estos son máximos absolutos
Si el extremo inferior es un valor finito, la función está acotada inferiormente. Si, además, la función alcanza su ínfimo en uno o varios puntos, estos son mínimos absolutos

Para estudiar la acotación de funciones continuas podemos utilizar el teorema de acotación, que veremos en niveles más avanzados.

Simetría

También llamada paridad, la simetría hace referencia a la correspondencia exacta entre dos partes de una función. Se puede distinguir entre simetría par o impar.

Decimos que una función presenta simetría par cuándo es simétrica respecto del eje de ordenadas y . Esto quiere decir que para cualquier x∈Dom_f, se cumple:

f (x) = f (- x)

Funciones simétricas pares y método gráfico para su identificación

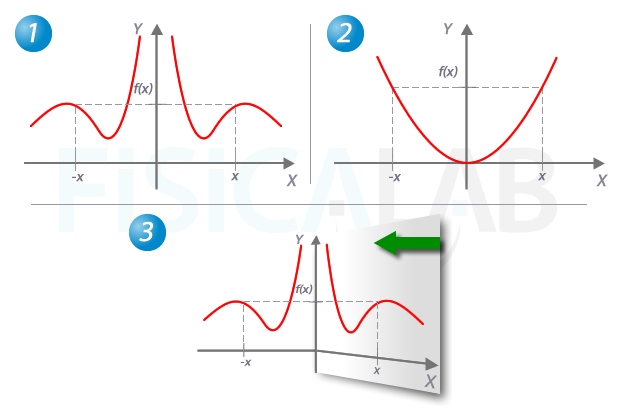
Simetría par

Arriba, en 1 y en 2, dos funciones simétricas respecto al eje y. Observa que cada valor x, tiene un valor -x, ambos en el dominio de la función, con igual imagen, es decir, f(x)=f(-x). Dicho de otra manera, si existe (x,f(x)), también existe (-x,f(x)). Por otro lado, tal y como se refleja en 3, para identificar las funciones de simetría par, puedes doblar, imaginariamente, la hoja por el eje y. Si las dos mitades de la función coinciden exactamente, la función es simétrica.

Decimos que una función presenta simetría impar cuándo es simétrica respecto del origen. Esto quiere decir que para cualquier x∈Dom_f, se cumple:

- f (x) = f (- x)

Funciones simétricas impares y método gráfico para su identificación

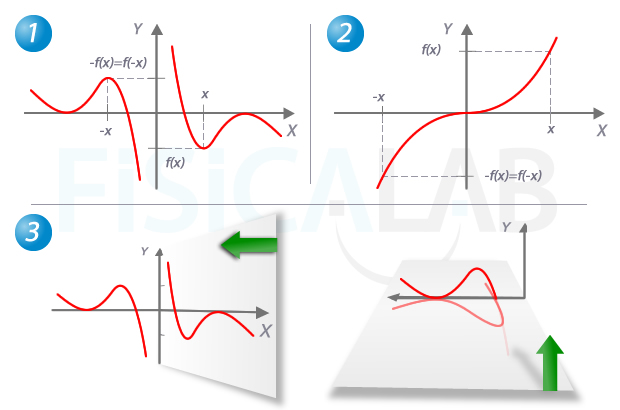
Simetría impar

Arriba, en 1 y en 2, dos funciones simétricas respecto al origen. Observa que cada valor x, tiene un valor -x, ambos en el dominio de la función, con imagen opuesta, es decir, f(-x)=-f(x). Dicho de otra manera, si existe (x,f(x)), también existe (-x,-f(x)). Por otro lado, tal y como se refleja en 3, para identificar las funciones de simetría impar, puedes doblar, imaginariamente, la hoja dos veces. Una por el eje y y otra por el eje x. Si, tras girar 180º cada vez, las partes coinciden exactamente, la función es simétrica.

Existen funciones que son simétricas respecto a otros ejes distintos del eje x o del origen. También existen funciones que simplemente no son simétricas en absoluto.

En resumen, para calcular la simetría par o impar de una función cualquiera:

Si tenemos su expresión analítica, calculamos f(-x). Si coincide con f(x) es simétrica par. Si coincide con -f(x) es simétrica impar
Si tenemos su gráfica seguimos el método señalado de doblar la hoja "mentalmente". Si obtenemos coincidencia al doblar por el eje y, tenemos simetría par. Si no, volvemos a doblar por el eje x y si hay coincidencia esta vez, tenemos simetría impar

Periodicidad

Decimos que una función es periódica cuando su forma se repite cada cierto intervalo llamado periodo. Formalmente:

Una función es periódica de período T si cumple que f(x)=f(x+T) para todo x∈Dom_f.

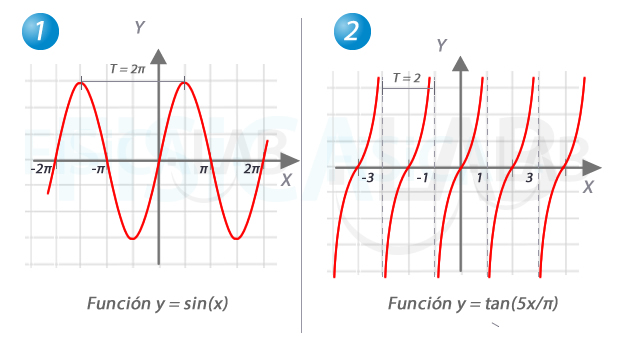
Funciones periódicas

Las funciones trigonométricas son habitualmente periódicas. A la izquierda, en 1, la función seno. Vemos que la forma se repite cada 2π. A la derecha, una variante de la función tangente, cuyo periodo es 2.

Si lo piensas un poco, te darás cuenta que una función que se repite cada T, también se repite cada 2·T, 3·T y así sucesivamente. T sería, por tanto, el período mínimo de repetición, es decir, su período fundamental.

Para calcular si una función es periódica:

Si tenemos la expresión analítica partimos de f(x+T) y estudiamos si existe algún T que haga f(x+T)=f(x). Si existe, la función es periódica
Si lo que tenemos es la gráfica de la función, buscamos si la forma se repite cada cierto intervalo. Si es así, es periódica, y la longitud del intervalo es el período T

Conclusión

En este apartado hemos introducido distintos conceptos que te van a permitir describir con mayor precisión las funciones. Algunos de ellos los hemos trabajado, fundamentalmente, desde un punto de vista gráfico. Cuando te familiarices con estos conceptos y conozcas las derivadas, podremos sistematizar un poco más su estudio. Además, para entonces podremos presentarte otros conceptos que también se usan en el análisis de funciones, como la continuidad, la derivabilidad o las asíntotas. Por ahora te recomendamos que practiques con los ejercicios de este apartado.

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.

Análisis de Funciones

Compartir en...

Síguenos en...

Dominio

Recorrido

Ceros

Signo

Monotonía

Crecimiento y decrecimiento

Criterio de la recta tangente

Máximos y mínimos

Curvatura

Concavidad

Convexidad

Criterio de la recta tangente

Puntos de inflexión

Acotación

Simetría

Periodicidad

Conclusión

Y ahora... ¡Ponte a prueba!

José L. Fernández

Apartados relacionados

Navegación