Teorema de Acotación
Ya hemos estudiado qué significa que una función esté acotada.
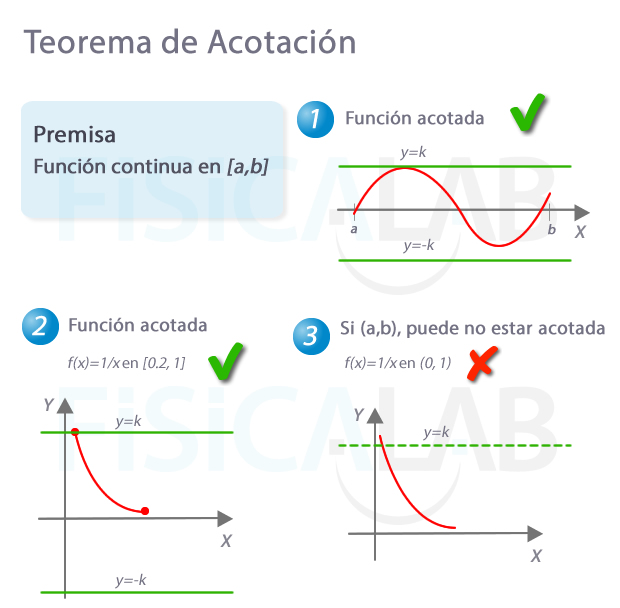
El teorema de acotación establece que toda función f(x) continua en el intervalo cerrado [a, b] está acotada en él.
El teorema establece que una función continua en un intervalo cerrado está acotada, pero no que una función acotada en en un intervalo cerrado sea continua en él. Como ejemplo de esto puedes reflexionar sobre qué le ocurre a la función f(x)=sin(1/x) en el intervalo [-1, 1].
Demostración
Para demostrar el teorema de acotación nos basaremos en las dos ideas siguientes, similares a las que utilizamos para demostrar el teorema de Bolzano:
-
Teorema de los intervalos encajados
Sea una sucesión de intervalos cerrados I1=[a1,b1], I2=[a2,b2], I3=[a3,b3]... In=[an,bn], tales que I1⊃I2⊃I3...⊃In y las longitudes de los mismos bn-an tiende a 0. Existe entonces un único valor c que es común a todos ellos. Matemáticamente:
-
Propiedad de las funciones continuas
Basándonos en la propia definición de función continua, sabemos que cuando una función es continua en un punto x0, existe un entorno de x0 en el que la función está acotada
A partir de aquí, comenzamos suponiendo un intervalo [a,b] en el que la función no está acotada. Su punto medio, c1 da lugar a dos subintervalos [a, c1], y [c1, b]. En uno ellos, al menos, la fución no está acotada (de estarlo en los dos, la fución estaría acotada en [a,b] y hemos supuesto que no lo está). A ese subintervalo lo llamamos [a1,b1].
Repetimos el razonamiento para ese [a1,b1] , considerando el punto medio c2, que a su vez da lugar a dos subintervalos de [a1,b1] en uno de los cuales la función no está acotada. Repitiendo el proceso, podemos afirmar que tenemos una sucesión de intervalos encajados en los que la función no está acotada, cuya longitud viene dada por la expresión
Sabemos que la función es continua en c, y por la propia definición de función continua debe existir un entorno en el que la función está acotada. Llamaremos a dicho entorno (c-δ, c+δ). En dicho entorno existen infinitos subtintervalos de la sucesión anterior (cuyas longitudes tendían a 0). En ellos la función no estaba acotada, lo cual se contradice con la propiedad de las funciones continuas, con lo cual hemos llegado a una contradicción. No queda más remedio que afirmar que la hipótesis de partida, es decir, que una función continua en [a,b] no está acotada, no es posible. Esto es justo lo que queríamos demostrar
El teorema de acotación es la base de la demostración que haremos del teorema de Weierstrass.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.