Extremos de una Función

Intuitivamente, los extremos de una función son los puntos más grandes o más pequeños de la función en su entorno. A los más grandes los llamamos máximos, y a los más pequeños mínimos (como ves, un derroche de originalidad). Ambos pueden ser absolutos o relativos. Aunque ya los introdujimos al estudiar la monotonía, en el análisis de funciones, en este apartado vamos a sistematizar su cálculo a través del uso de las derivadas. 

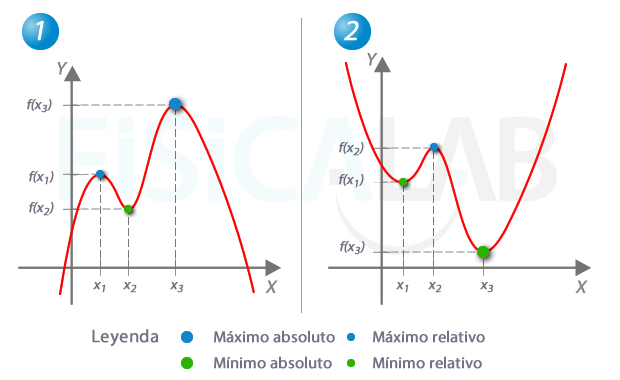
Tipos de extremos de una función

Los extremos de una función pueden clasificarse:

• Máximos y mínimos
• Locales (o relativos) y absolutos.

Observa en la imagen los extremos señalados. ¿Serías capaz de identificar qué ocurre a la recta tangente en ellos y en su entorno?

En este apartado vamos a estudiar:

• Qué son los puntos críticos, y los singulares, y su relación con la monotonía de una función
• Cómo identificar máximos
• Cómo identificar mínimos
• Cómo identificar puntos silla
• Regla práctica para el cálculo de máximos y mínimos

¿Empezamos?

Puntos críticos y monotonía de una función 

Un punto crítico es aquel en el que la función podría cambiar su monotonía, es decir, su tendencia a crecer o a decrecer.  En los puntos críticos se puede encontrar un máximo, un mínimo o ninguna de las dos cosas. Se trata por tanto de puntos que debemos estudiar con atención cuando queramos averiguar los extremos de la función. 

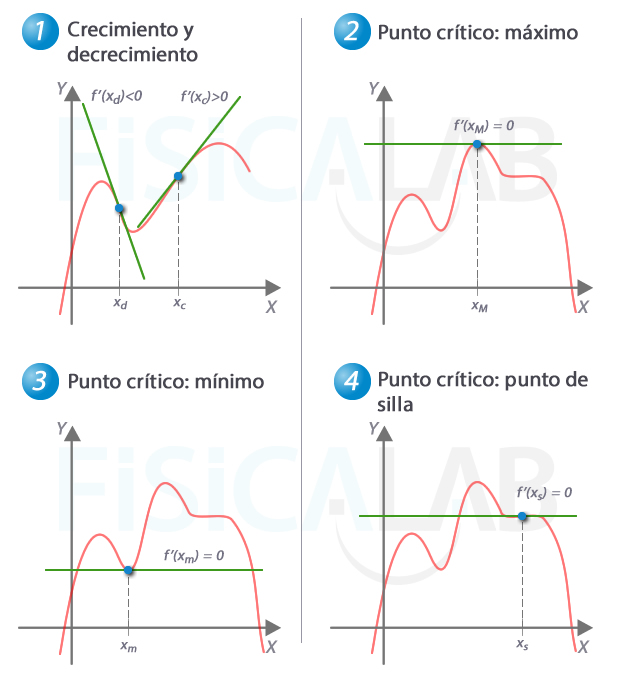
Criterio de la recta tangente

El valor de la pendiente de la recta tangente en un punto en el que la función es derivable, nos dice si la función crece en ese punto, decrece, o es un punto crítico. Así:

• En 1 vemos un punto x_d en el que la función 'va hacia abajo' (decrece), y otro x_c en el que 'va hacia arriba' (crece)
• En 2, 3 y 4 observamos distintos puntos críticos. En todos ellos la pendiente de la recta tangente vale 0. En x_M hay un máximo, en x_m un mínimo, y en x_s un punto de silla (un punto de tangente 0, pero en el que la función sigue siendo creciente o decreciente, es decir en el que la tendencia de crecimiento de la función no cambia)

Si en todos los puntos críticos el valor de la derivada es 0, ¿se te ocurre cómo distinguirlos?

Si lo que quieres es resolver cuanto antes la duda de cómo distinguir los puntos críticos (máximos, de mínimos y de puntos silla), puedes saltar la demostración siguiente... En cualquier caso, si eres de los que gusta de llegar hasta el fondo de las cosas, te recomendamos que sigas leyendo.

Demostración

Tal y como vimos al explicar el análisis de una función, el crecimiento o decrecimiento de una función está asociado a un intervalo. Por tanto, para asociar dicha idea a un punto, debemos hacer el intervalo infinitamente pequeño en el entorno de dicho punto, que llamaremos x=a.

En primer lugar, vamos a demostrar que si f es creciente en x=a, entonces f'(a)≥0.

1. La función f es creciente en x=a cuando podemos encontrar un entorno de x=a en el que el signo de [f(a+h)-f(a)] = signo de h, con -lim<h<lim y h≠0

   

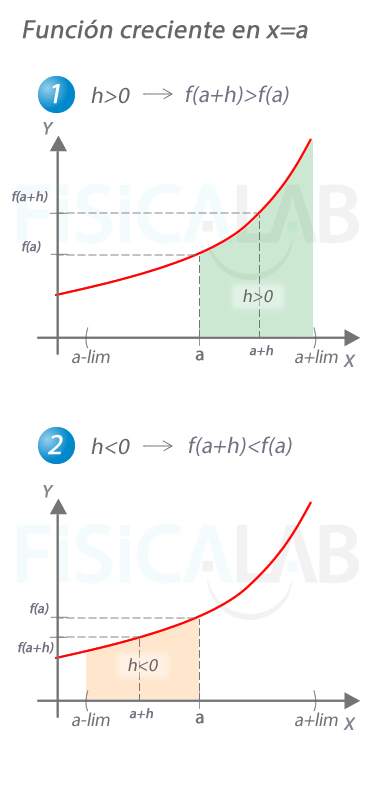
   Función creciente en un punto

   La función de la imagen es creciente en x=a. Observa que existe un entorno del punto considerado, (a-lim, a+lim) en el que, para cualquier x=a+h de su interior se cumple que:

   1. Si h>0, entonces f(a+h)-f(a)>0
   2. Si h<0, entonces f(a+h)-f(a)<0

   En definitiva, podemos decir que signo de h = signo [f(a+h)-f(a)]

2. A partir de lo anterior, podemos afirmar que en una función creciente en x=a, el cociente $\frac{f\left(a+h\right)-f\left(a\right)}{h}>0$, ya que los signos del numerador y del denominador coincidirán

3. Recordando la definición de derivada, y que el límite de una función positiva es positivo o nulo podemos escribir:

   $$f\text{'}\left(a\right)=\underset{h\to 0}{\lim }\frac{f\left(a+h\right)-f\left(a\right)}{h}\ge 0$$

Ahora vamos a demostrar que si f es decreciente en x=a, entonces f'(a)≤0.

1. La función f es decreciente en x=a cuando podemos encontrar un entorno de x=a en el que el signo de [f(x+h)-f(x)] ≠ signo de h, con -lim<h<lim y h≠0

   

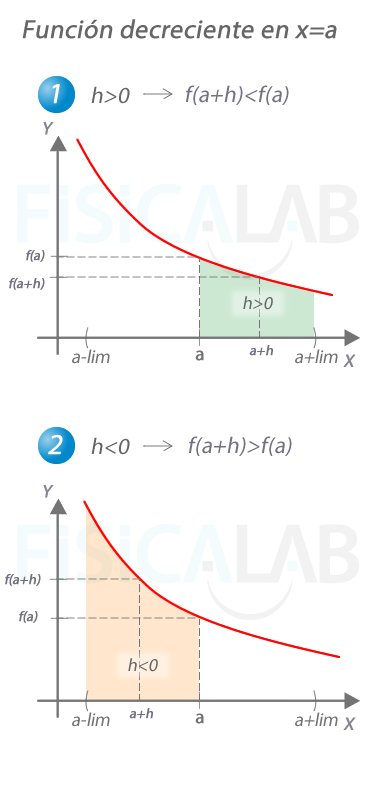
   Función decreciente en un punto

   La función de la imagen es decreciente en x=a, esto es, existe un entorno del punto considerado, (a-lim, a+lim) en el que, para cualquier x=a+h de su interior se cumple que:

   1. Si h>0, entonces f(a+h)-f(a)<0
   2. Si h<0, entonces f(a+h)-f(a)>0

   Así pues, podemos decir que signo de h = [f(a+h)-f(a)]

2. A partir de lo anterior, podemos afirmar que en una función decreciente en x=a, el cociente $\frac{f\left(a+h\right)-f\left(a\right)}{h}<0$, ya que los signos del numerador y del denominador son complementarios.

3. Recordando la definición de derivada, y que el límite de una función negativa es negativo o nulo podemos escribir:

   $$f\text{'}\left(a\right)=\underset{h\to 0}{\lim }\frac{f\left(a+h\right)-f\left(a\right)}{h}\le 0$$

Máximos

De manera intuitiva, una función tiene un máximo relativo en x=x_M cuando el valor de la misma en el punto, f(x_M), es mayor que en los puntos de su entorno. Puedes utilizar la siguiente regla práctica para la identificación de máximos relativos.

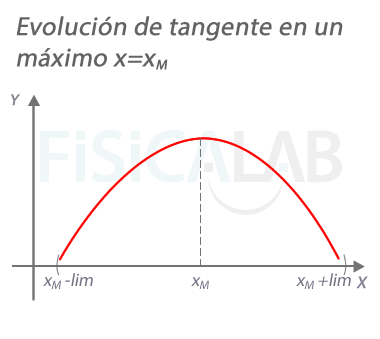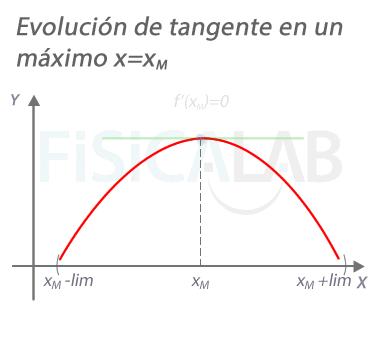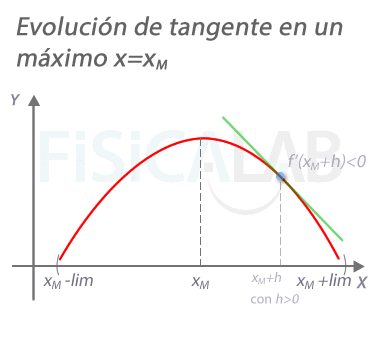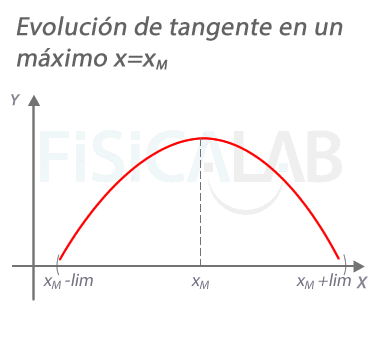
Evolución de la recta tangente en un máximo

En un máximo x_M, la pendiente de la recta tangente a la función vale 0. A la izquierda del mismo, en un punto próximo x_M+h con h<0 la pendiente es positiva. A la derecha, en un punto próximo x_M+h con h>0, la pendiente es negativa.

Demostración

Como el valor de la función en x=x_M es mayor que en cualquier punto de su entorno próximo, se cumple que f(x_M)-f(x_M+h)>0, para cualquier h∈ℝ, con -lim<h<lim y h≠0.

• Si $h>0\Rightarrow \frac{f\left(x_M\right)-f\left(x_M+h\right)}{h}>0\Rightarrow f\text{'}\left({x_M}^{+}\right)=\underset{h\to 0^{+}}{\lim }\frac{f\left(x_M\right)-f\left(x_M+h\right)}{h}\ge 0$
• Si $h<0\Rightarrow \frac{f\left(x_M\right)-f\left(x_M+h\right)}{h}<0\Rightarrow f\text{'}\left({x_M}^{-}\right)=\underset{h\to 0^{-}}{\lim }\frac{f\left(x_M\right)-f\left(x_M+h\right)}{h}\le 0$

Como la función es derivable en x=x_M, las derivadas laterales deben coincidir, y por tanto la única posibilidad es que f'(x_M^-)=f'(x_M⁺)=f'(_M)=0.

Máximos absolutos

Una función tiene un máximo absoluto en x=M cuando f(M), es mayor o igual que cualquier otra imagen de la función. Es decir, cuando f(M)⩾f(x) para cualquier x≠M perteneciente al dominio de la función. Por tanto, los máximos absolutos se pueden encontrar:

• Entre los máximos relativos
• En los extremos del dominio de la función

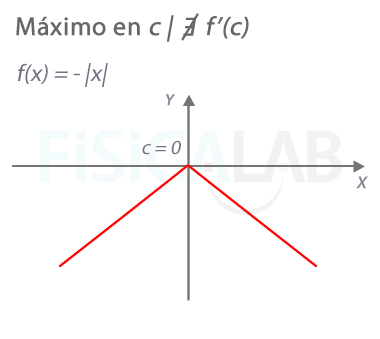
Máximo en punto en que la función no es derivable

En la imagen representamos la función valor absoluto cambiada de signo: f(x)=-|x|. En ella ∄f'(0), siendo sin embargo x=0 un máximo absoluto.

Mínimos

Análogamente, una función tiene un mínimo relativo en x=x_m cuando el valor de la misma en el punto, f(x_m), es menor que en los puntos de su entorno. Cuando el valor de la función en el mínimo, f(x_m), es menor o igual que cualquier otra imagen de la función, entonces en x=x_m hay un mínimo absoluto. De nuevo, podemos usar la siguiente regla práctica para la identificación de mínimos.

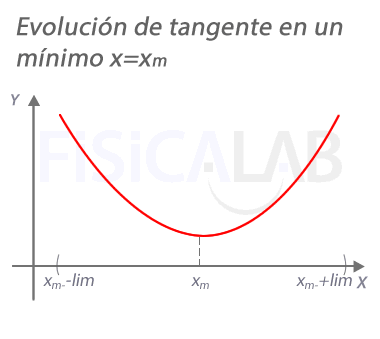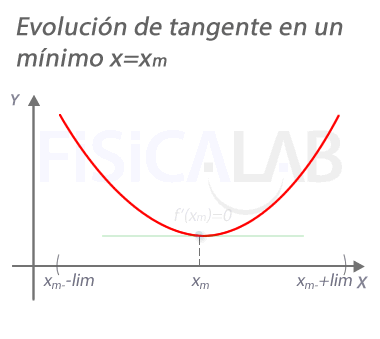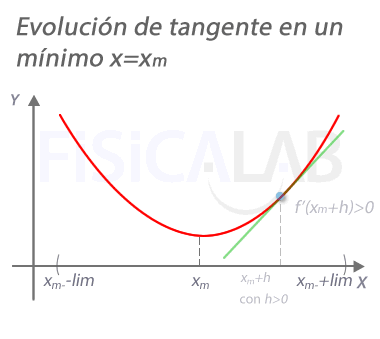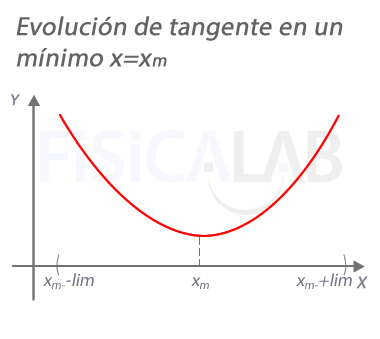
Evolución de la recta tangente en un mínimo

En un máximo x_m, la pendiente de la recta tangente a la función vale 0. A la izquierda del mismo, en un punto próximo x_m+h con h<0 la pendiente es negativa. A la derecha, en un punto próximo x_M+h con h>0, la pendiente es positiva.

Demostración

Como el valor de la función en x=x_m es menor que en cualquier punto de su entorno próximo, se cumple que f(x_m)-f(x_m+h)<0, para cualquier h∈ℝ, con -lim<h<lim y h≠0.

• Si $h>0\Rightarrow \frac{f\left(x_m\right)-f\left(x_m+h\right)}{h}<0\Rightarrow f\text{'}\left({x_m}^{+}\right)=\underset{h\to 0^{+}}{\lim }\frac{f\left(x_m\right)-f\left(x_m+h\right)}{h}\le 0$
• Si $h<0\Rightarrow \frac{f\left(x_m\right)-f\left(x_m+h\right)}{h}>0\Rightarrow f\text{'}\left({x_m}^{-}\right)=\underset{h\to 0^{-}}{\lim }\frac{f\left(x_m\right)-f\left(x_m+h\right)}{h}\ge 0$

Como la función es derivable en x=x_m, las derivadas laterales deben coincidir, y por tanto la única posibilidad es que f'(x_m^-)=f'(x_m⁺)=f'(x_m)=0.

Mínimos absolutos

Una función tiene un mínimo absoluto en x=m cuando f(m), es menor o igual que cualquier otra imagen de la función. Es decir, cuando f(m)⩽f(x) para cualquier x≠m perteneciente al dominio de la función. Por tanto, los mínimos absolutos se pueden encontrar:

• Entre los mínimos relativos
• En los extremos del dominio de la función

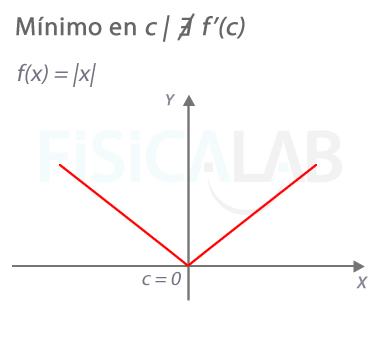
Mínimo en punto en que la función no es derivable

En la imagen representamos la función valor absoluto: f(x)=|x|. En ella ∄f'(0), siendo sin embargo x=0 un mínimo absoluto.

Puntos silla

Cuando la derivadas a la izquierda y a la derecha de las proximidades de un punto x=x_s en el que f'(x_s)=0 tengan el mismo signo, la función tiene un punto silla en él. A estos puntos también se les llama puntos de ensilladura, por la similitud que tiene la gráfica de la función en ellos con una representación tosca de una silla.

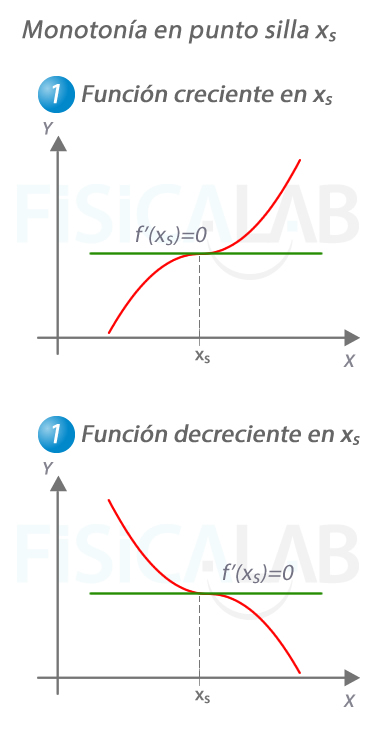
Monotonía de una función en un punto silla

En la imagen tienes dos funciones distintas, en 1 y en 2. En ambas existe un punto de silla, en el que la pendiente de la recta tangente f'(x_s) vale 0. En ambos casos, la pendiente de la recta tangente a la izquierda y a la derecha de x_s tiene el mismo signo.

• En 1, la función es creciente en x_s ya que la pendiente de la recta tangente a la izquierda y a la derecha es positiva
• En 2, la función es decreciente en x_s ya que la pendiente de la recta tangente a la izquierda y a la derecha es negativa

Regla práctica

Aplicando los criterios prácticos presentados hasta ahora, debería ser inmediato saber si una función es creciente, decreciente o presenta un extremo relativo en un punto dado. La dificultad estriba en saber obtener sus intervalos de crecimiento, decrecimiento, y los puntos que son extremos absolutos y relativos cuando te proporcionan únicamente la función. Te recomendamos que sigas los siguientes pasos:

1. Determinar el dominio de la función, para asegurarnos que los puntos que vamos a obtener pertenecen al mismo

2. Determina la expresión de la primera derivada de la función

3. Obtén los puntos críticos de la función a partir de su derivada:

   • Los puntos singulares, esto es, los puntos que hacen f'(x)=0

   • Los puntos en los que ∄ f'(x)

4. Estudia el signo de dicha función derivada, ayudándote de un cuadro de signos. Coloca en dicho cuadro, sobre el dominio de la función, los puntos críticos obtenidos, y en cada intervalo resultante determina el signo de la derivada

5. En los intervalos de signo positivo, la función original crece. En los intervalos de signo negativo, la función decrece

6. En los puntos críticos en los que haya un cambio de tendencia (de crecimiento a decrecimiento o viceversa) habrá extremos relativos (máximos o mínimos). Adicionalmente, también puedes comprobar si un punto es un máximo o un mínimo con el criterio de la segunda derivada, que presentaremos al estudiar la curvatura de la funciones

7. En los puntos críticos en los que la tendencia se mantenga, habrá puntos silla

8. En cuanto a los máximos y mínimos absolutos, de haberlos, estos se encontrarán entre los extremos relativos y los extremos del dominio. Para evaluarlos debemos hacer un estudio más detallado, realizando un esbozo de la función que nos permita conocer sus asíntotas, ramas parabólicas, etc.

   Ten presente que si la función es continua y está definida en un intervalo cerrado [a,b], el estudio se simplifica. Como estudiarmos al presentar el Teorema de Weierstrass, una función continua en un intervalo cerrado alcanzará su máximo absoluto y su mínimo absoluto en dicho intervalo. Por tanto los máximos y mínimos absolutos estarán necesariamente entre los relativos obtenidos y los extremos del intervalo. Basta calcular la imagen de la función en ellos para obtenerlos.

Te recomendamos que realices los ejercicios asociados a este apartado para poder asimilar estas ideas. ¡Verás que es muy sencillo!