Producto Vectorial
El producto vectorial de un vector
- Módulo :
- Dirección : Es perpendicular al plano que definen ambos vectores
- Sentido : Queda definido por cualquiera de las siguientes reglas:
- Regla del sacacorchos o del tornillo. El sentido es el mismo sentido de avance de un sacacorchos o tornillo que girase desde
- Regla de la mano derecha con la palma. También puedes utilizar la palma de tu mano, orientándola desde
- Regla de la mano derecha con tres dedos. Otra opción es utilizar tu mano derecha y los dedos índice (
- Regla del sacacorchos o del tornillo. El sentido es el mismo sentido de avance de un sacacorchos o tornillo que girase desde
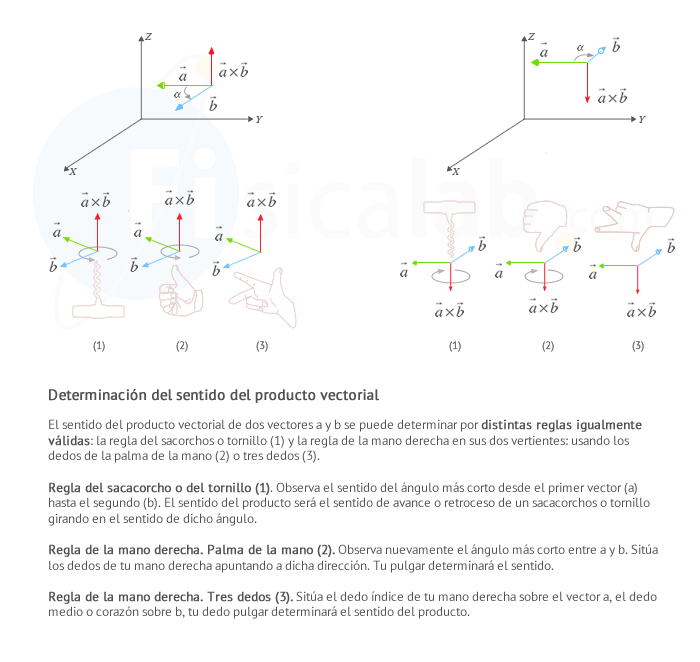
Como puedes observar, el producto vectorial no es conmutativo (
Expresión analítica
La expresión analítica del producto vectorial
Donde:
Comprobación
Para realizar la comprobación de la expresión anterior debes de tener en cuenta que:
-
el módulo del producto vectorial de un vector a por sí mismo es
-
por otro lado, teniendo en cuenta que la dirección del producto vectorial es perpendicular al plano que definen los vectores, y la propiedad anticonmutativa, nos queda:
Finalmente, usando la propiedad distributiva a partir de las componentes cartesianas, nos queda:
¿Qué pasa si los vectores son sólo de dos componentes?
En ocasiones, para simplificar cálculos, solemos trabajar con vectores en dos dimensiones. Teniendo en cuenta que la dirección del producto vectorial es siempre perpendicular al plano que forman los vectores, necesitaremos una tercera dimensión para poder expresarlo. Para obtener la expresión analítica podemos suponer que la componente z de cada vector es cero, tal y como hacemos en el siguiente ejercicio.
Área del paralelogramo
Geométricamente, el módulo del producto vectorial tiene igual valor que el área del paralelogramo obtenido a partir de los vectores
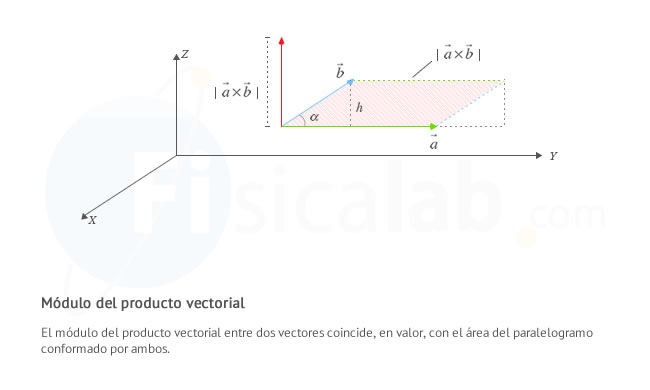
Observa que:
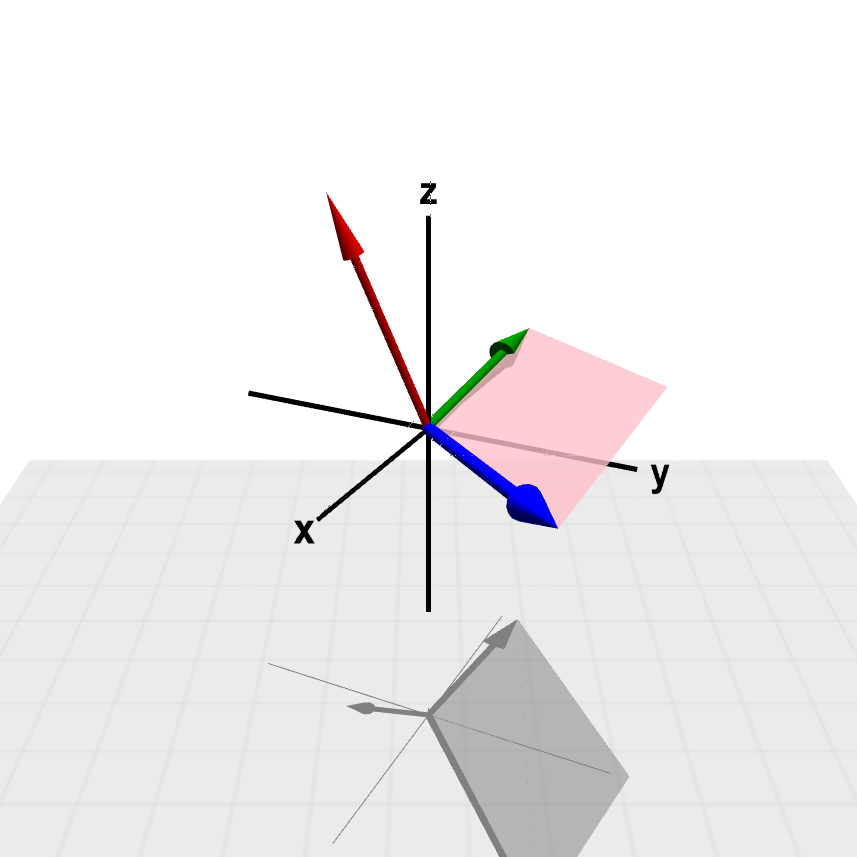
Representación en tres dimensiones
En el siguiente experimenta y aprende se representa el producto vectorial en el espacio. Aunque resulta algo difícil de manipular, sirve para que puedas ver con claridad como functiona esta operación y entiendas las propiedades que hemos tratado.
Conclusión
En este apartado hemos presentado el producto vectorial. En física necesitamos 3 dimensiones para expresarlo. Dependiendo del problema concreto al que nos enfrentemos podemos expresar el producto vectorial
- como un módulo r y un vector unitario
- según sus componentes cartesianas, a partir de la expresión analítica (determinante 3x3),
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.