Aceleración Tangencial
En Física decimos que un cuerpo tiene aceleración cuando se produce un cambio del vector velocidad, ya sea en módulo o dirección. En apartados anteriores hemos visto que la aceleración se puede clasificar según el efecto que produce en la velocidad en aceleración tangencial (si hace que cambie el módulo del vector velocidad) y aceleración normal o centrípeta (si hace que cambie su dirección). Son las componentes intrínsecas de la aceleración. En este apartado vamos a desarrollar con mayor profundidad el concepto de aceleración tangencial.
Aceleración tangencial
Con anterioridad hemos visto que la aceleración instantánea es la derivada de la velocidad respecto al tiempo. Por otro lado, hemos visto que podemos expresar el vector velocidad como el producto de su módulo por un vector unitario tangente a la trayectoria:
Donde hemos aplicado la regla de derivación de un producto D(ab)=a'b+ab'.
Vemos que el primer término (
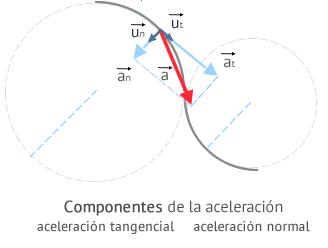
La aceleración tangencial mide los cambios del módulo de la velocidad en el tiempo. Su expresión viene dada por:
Donde:
El valor de la aceleración tangencial puede ser:
- Mayor que cero (> 0): Cuando el cuerpo tiene un movimiento acelerado, es decir, el módulo del vector velocidad aumenta con el tiempo
- Menor que cero (<0): Cuando el cuerpo tiene un movimiento retardado o decelerado, es decir, el módulo del vector velocidad disminuye con el tiempo
- Igual a cero (= 0): Cuando el cuerpo tiene un movimiento uniforme, es decir, el módulo del vector velocidad permanece constante
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
