¿Hacia que lado se inclina la palanca?
Enunciado
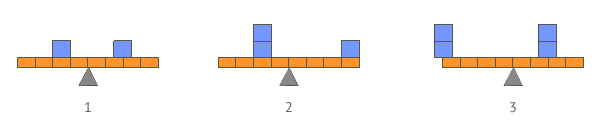
Indica hacia qué lado se moverá cada palanca, inicialmente en reposo, si cada cuadrado azul pesa m kg y cada segmento mide l m. (Datos: g = 10 m/s2)
Solución
Consideraciones previas
Dado que los cuadrados no son masas puntuales consideraremos que su peso se ubica en su centro de gravedad (cdg). El cdg de un cuadrado homogéneo es su centro de geométrico. Llamaremos m1 a la masa o conjunto de masas situados a la izquierda de la palanca y m2 a las de la derecha.
Para saber hacia que lado se inclinará la palanca deberemos determinar el momento más grande del peso de ambas masas. Llamaremos M1 al momento de P1 y M2 al momento de P2.
- Si M1 > M2 la palanca se inclina hacia m1.
- Si M1 = M2 la palanca se quedará como está.
- Si M1 < M2 la palanca se inclinará hacia m2.
Caso 1)
Datos
m1 = m kg
m2 = m kg
P1 = m1 · g = 10 · m kg
P2 = m2 · g = 10 · m kg
d1 = 1.5 · l m
d2 = 2 · l m
Resolución
Caso 2)
Datos
m1 = 2m kg
m2 = m kg
P1 = m1 · g = 10 · 2m kg
P2 = m2 · g = 10 · m kg
d1 = 1.5 · l m
d2 = 3.5 · l m
Resolución
Caso 3)
Datos
m1 = 2m kg
m2 = 2m kg
P1 = m1 · g = 10 · 2m kg
P2 = m2 · g = 10 · 2m kg
d1 = 4 · l m
d2 = 2 · l m
Resolución
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
