Gráficas Movimiento Rectilíneo Uniforme (M.R.U.)
Un cuerpo realiza un movimiento rectilíneo uniforme cuando su trayectoria es una línea recta y su velocidad es constante. En este apartado vamos a estudiar las gráficas del m.r.u, es decir:
Gráficas de M.R.U.
Gráfica posición-tiempo (x-t)
La gráfica posición-tiempo (x-t) de un movimiento rectilíneo uniforme (m.r.u.). representa en el eje horizontal (eje x) el tiempo y en el eje vertical la posición. Observa como la posición (normalmente la coordenada x) aumenta (o disminuye) de manera uniforme con el paso del tiempo. Podemos distinguir dos casos, cuando la velocidad es positiva o negativa:
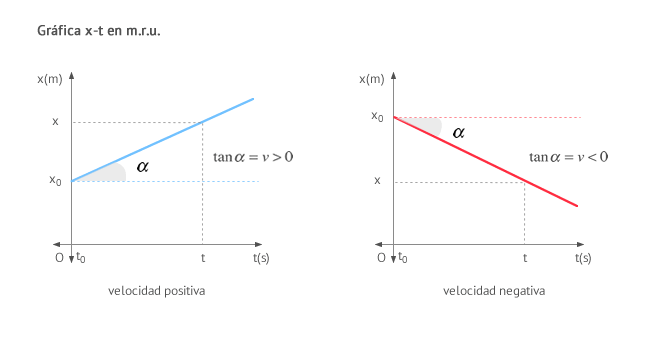
A partir del ángulo α puedes obtener la velocidad. Recuerda para ello que, en un triángulo rectángulo se define la tangente de uno de sus ángulos como el cateto opuesto partido cateto contiguo:
El valor de la pendiente es la propia velocidad. Por tanto a mayor pendiente de la recta, mayor velocidad posee el cuerpo.
Gráfica velocidad-tiempo (v-t)
La gráfica velocidad-tiempo (v-t) de un movimiento rectilíneo uniforme (m.r.u.) muestra que la velocidad permanece constante a lo largo del tiempo. De nuevo, podemos distinguir dos casos:
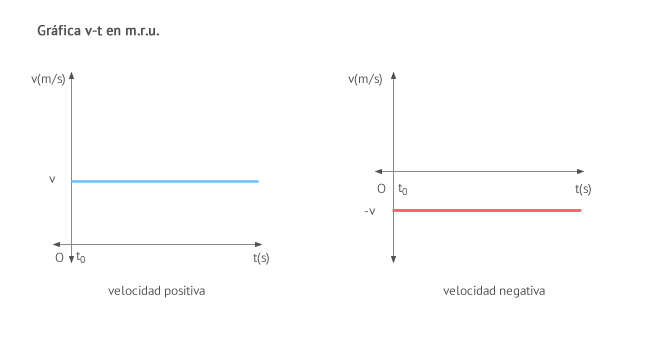
Observa que el área que limitada bajo la curva v entre dos instantes de tiempo es el espacio recorrido.
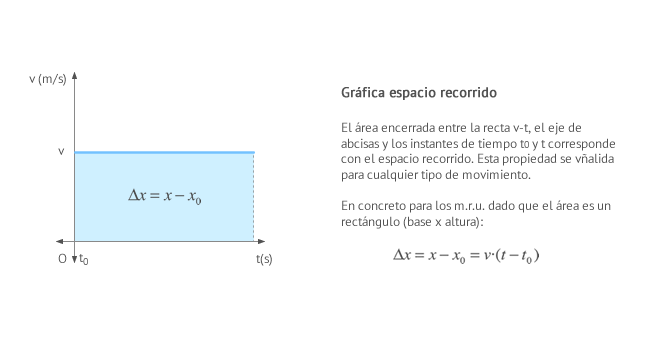
En este caso resulta inmediato calcular dicha área, al tratarse de un rectángulo. Pero, ¿sabrías qué herramienta matemática permite el cálculo de áreas bajo una curva, sea cual sea su forma?
Gráfica aceleración-tiempo (a-t)
La gráfica aceleración-tiempo (a-t) de un movimiento rectilíneo uniforme (m.r.u.) muestra que la aceleración es nula en todo momento. En este caso, tanto si la velocidad del cuerpo se considera positiva como negativa, tenemos una sola posibilidad, ilustrada en la figura:
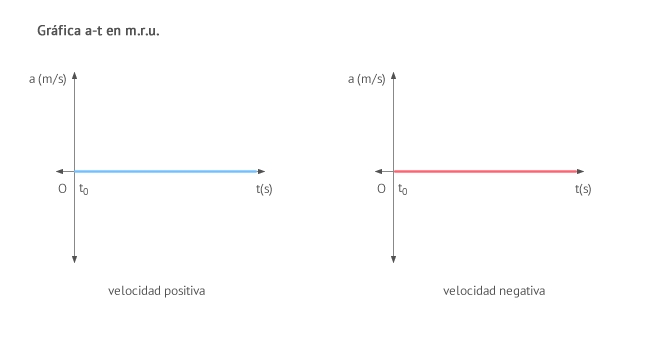
Y ahora... ¡Ponte a prueba!
Apartados relacionados
Este mismo apartado se encuentra desarrollado en otros niveles educativos. Si sus contenidos no se ajustan al nivel que buscas, prueba a visitar:
