Reflexión total para rayos de luz en benceno

Datos

• Profundidad del depósito: h = 4 m
• Índice de refracción absoluto del benceno a la longitud de onda considerada n_b = 1.501

Consideraciones previas

Sabemos que cuando la luz pasa del benceno al aire los rayos se refractarán. La bombilla de luz será visible para un observador situado en el exterior del depósito siempre que algún rayo de los refractados pueda incidir sobre la retina del mismo. Sin embargo, el enunciado nos indica explícitamente que, una vez situado el disco, la bombilla no es visible desde el exterior. ¿Cómo puede ser esto posible? Debemos recordar que cuando la luz pasa de un medio con un índice de refracción mayor a uno menor se produce, para ciertos ángulos de incidencia, la reflexión total (no hay ángulo refractado). A partir de aquí podemos hacer una representación de la situación:

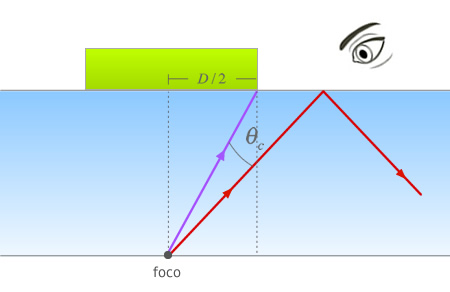
Como se pone de manifiesto en la imagen anterior, el radio del disco debe ser tal que tape todos los rayos de luz en los que no se produzca reflexión total (el rayo morado marca el límite superior o ángulo máximo que puede tener un rayo sin que se produzca reflexión total). El resto de rayos, que saldrían refractados a la derecha y a la izquierda del disco, como por ejemplo el rojo, tienen un ángulo de incidencia mayor que el ángulo crítico, con lo que quedarían atrapados en el benceno.

Resolución

Comenzamos calculando el ángulo crítico o ángulo límite según:

$${\theta }_c=arcsen\left(\frac{n_2}{n_1}\right)=arcsen\left(\frac{1}{1.501}\right)=0.729 rad$$ 

A partir de el ángulo crítico, y del triángulo rectángulo definido podemos escribir:

$$\tan \left({\theta }_c\right)=\frac{D/2}{4}\Rightarrow 8·\tan \left({\theta }_c\right)=D\Rightarrow D=7.14 m$$