Razones Trigonométricas de los Ángulos de 30º, 45º y 60º

A los ángulos de 30º, 45º y 60º (ó sus equivalentes en radianes π/6 rad, π/4 rad y π/3 rad) se les conoce como ángulos notables. Se llaman así porque aparecen muy a menudo en nuestra vida cotidiana, y resulta de gran utilidad aprender de memoria los valores de sus razones trigonométricas. De hecho, es posible calcular el valor de las razones de otros ángulos a partir de estas. En este apartado vamos a estudiar:

Deducción de las razones de 30º y 60º (ó π/6 rad y π/3 rad respectivamente)
- Valor de las razones de 60º (ó π/3 rad)
- Valor der las razones de 30º (ó π/6 rad)
Deducción de las razones de 45º (ó π/4 rad)
- Su valor
Razones de otros ángulos notables

¿Preparado para triangularizar tu mente?

Recuerda que también puedes obtener el valor de las razones que vamos a estudiar mediante una calculadora. Simplemente introduce el ángulo deseado, en grados o radianes, y pulsa la tecla correspondiente , ó .

Cómo deducir razones de los ángulos de 30º y 60º

Si cogemos un triángulo equilatero ABC, que como recordarás tiene todos sus lados (l) y sus ángulos iguales (60º ó π/3 rad), y lo dividimos por la mitad obtendremos dos triángulos rectángulos.

Un triángulo equilatero se puede dividir en dos triángulos equiláteros,cada uno de ellos tendrá un ángulo de 30º, 60º y 90º

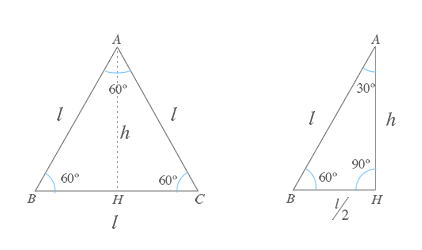
Descomposición de un triángulo equilatero

Al dividir por su altura un triángulo equilátero ABC como el de la figura obtendremos un triángulo rectángulo en el que los vértices A y B tendrán 30º (ó π/6 rad) y 60º (ó π/3 rad) respectivamente.

Si conocemos el valor de los lados l, podemos calcular el valor de la altura por medio del teorema de Pitágoras:

$l^{2} = h^{2} + {(\frac{l}{2})}^{2}; h = \sqrt{l^{2} - {(\frac{l}{2})}^{2}} = \sqrt{\frac{3}{4} \cdot l^{2}} = \frac{\sqrt{3}}{2} \cdot l$

A partir de esta figura y aplicando la definición de seno, coseno y tangente de cualquier ángulo agudo podemos obtener las razones trigonométricas de los ángulos de 30º y 60º (o sus equivalentes en radianes).

Razones trigonométricas de los ángulos de 60º

Razones	Razones inversas
$\sin 60 º = \frac{h}{l} = c o s 30 º = \frac{\sqrt{3}}{2}$	$cosec 60 º = \frac{l}{h} = s e c 30 º = \frac{2 \sqrt{3}}{3}$
$\cos 60 º = \frac{\frac{l}{2}}{l} = \sin 30 º = \frac{1}{2}$	$sec 60 º = \frac{l}{\frac{l}{2}} = cosec 30 º = 2$
$tg 60 º = \frac{h}{\frac{l}{2}} = c o t g 30 º = \sqrt{3}$	$cotg 60 º = \frac{\frac{l}{2}}{\frac{\sqrt{3}}{2} \cdot l} = t g 30 º = \frac{\sqrt{3}}{3}$

Razones trigonométricas de los ángulos de 30º

Razones	Razones inversas
$\sin 30 º = \frac{\frac{l}{2}}{l} = \cos 60 º = \frac{1}{2}$	$cosec 30 º = \frac{l}{\frac{l}{2}} = 2$
$\cos 30 º = \frac{h}{l} = \sin 60 º = \frac{\sqrt{3}}{2}$	$sec 30 º = \frac{l}{h} = \frac{2 \sqrt{3}}{3}$
$tg 30 º = \frac{\frac{l}{2}}{h} = cotg 60 º = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}$	$cotg 30 º = \frac{h}{\frac{l}{2}} = \sqrt{3}$

Cómo deducir razones de los ángulos de 45º

Para determinar las razones trigonométricas de un ángulo de 45º (o su equivalente π/4 rad) tomaremos un cuadrado de lado l y lo dividiremos por su diagonal provocando que aparezcan dos triángulos isósceles. Recuerda que un triángulo isósceles tiene dos ángulos de 45º y uno de 90º.

Un cuadrado se puede dividir en dos triángulos isósceles

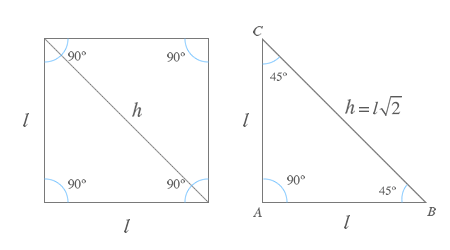
Descomposición de un cuadrado

Al dividir un cuadrado de lado l por su diagonal obtenemos dos triángulos isósceles cuya hipotenusa se puede obtener por medio del teorema de Pitágoras.

$h = \sqrt{l^{2} + l^{2}} = l \sqrt{2}$

Razones trigonométricas de los ángulos de 45º

Si aplicamos las definiciones de las distintas razones trigonométricas sobre el anterior triángulo isósceles obtenemos que:

Razones	Razones inversas
$\sin 45 º = \frac{l}{h} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$	$cosec 45 º = \frac{h}{l} = \sqrt{2}$
$\cos 45 º = \frac{l}{h} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$	$sec 45 º = \sqrt{2}$
$tg 45 º = \frac{l}{l} = 1$	$cotg 45 º = \frac{l}{l} = 1$

Razones trigonométricas de ángulos notables

Además de las razones ya vistas, existen otros ángulos cuyas razones son igualmente importantes. Se trata de los ángulos de 90º (ó π/2 rad), 180º (ó π rad) y 270º (ó 3π/2 rad). Profundizaremos sobre estos valores cuando estudiemos las razones trigonométricas de ángulos cualesquiera. Finalmente recuerda que las razones de 0º (0 rad) coinciden con las de 360º (ó 2π rad).

	0º	30º	45º	60º	90º	180º	270º
sen	$0$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	$1$	$0$	$- 1$
cos	$1$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	$0$	$- 1$	$0$
tg	$0$	$\frac{\sqrt{3}}{3}$	$1$	$\sqrt{3}$	$\infty$	$0$	$- \infty$
cosec	$\infty$	$2$	$\frac{2}{\sqrt{2}}$	$\frac{2}{\sqrt{3}}$	$1$	$\infty$	$- 1$
sec	$1$	$\frac{2}{\sqrt{3}}$	$\frac{2}{\sqrt{2}}$	$2$	$\infty$	$- 1$	$\infty$
cotg	$\infty$	$\frac{3}{\sqrt{3}}$	$1$	$\frac{1}{\sqrt{3}}$	$0$	$\infty$	$0$

Si observas la anterior tabla con atención puedes darte cuenta que para cualquier ángulo agudo se cumplen las siguientes ecuaciones:

$\sin α = \cos (90 º - α)$

$\cos α = \sin (90 º - α)$

$tg α = cotg (90 º - α)$

Ejemplo

Conociendo las razones trigonométricas de 30º, 45º y 60º calcular las razones trigonométricas de los siguientes ángulos:

a) sen 1470º
b) cos 405º
c) tan 13π/3

Ver solución

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.

Navegación