Imagen desde el interior de una pecera esférica

Datos

• Radio de la superficie del dioptrio (pecera) |R| = 65 cm = 6.5·10^-1 m
• Distancia del gato al dioptrio |s| = 30 cm = 3·10^-1 m
• Indice de refracción del agua n_agua = 1.33

Consideraciones previas

Observa que hemos indicado las magnitudes R y s en valores absolutos. La razón es que hasta que no situemos los distintos elementos en el plano, no podemos asignarle un signo, según el criterio DIN.

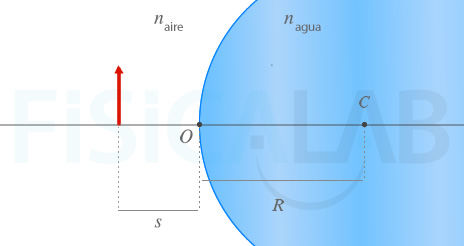
A partir de la imagen anterior, en la que el gato se ha representado por una flecha, podemos decir:

• R = 6.5·10^-1 m
• s = -3·10^-1 m

Además, debemos saber que n_aire = 1 . Con estos datos ya estamos en disposición de describir la imagen formada, estos es, la posición de la misma y su aumento.

Resolución

En primer lugar, aplicamos la ecuación fundamental del dioptrio esférico para determinar la posición de la imagen s' :

$$\begin{gathered} \frac{n\text{'}}{s\text{'}}-\frac{n}{s}=\frac{n\text{'}-n}{R}\Rightarrow \frac{1.33}{s\text{'}}-\frac{1}{-3·{10}^{-1}}=\frac{1.33-1}{6.5·{10}^{-1}}\Rightarrow \frac{1.33}{s\text{'}}=\frac{0.33}{6.5·{10}^{-1}}+\frac{1}{-3·{10}^{-1}}\Rightarrow \\ \Rightarrow \frac{1.33}{s\text{'}}=-2.83\Rightarrow s\text{'}=-0.46 m \end{gathered}$$ 

Seguimos calculando el aumento lateral:

$$A_L=\frac{y\text{'}}{y}=\frac{n·s\text{'}}{n\text{'}·s}=\frac{1·\left(-0.46\right)}{1.33·\left(-0.3\right)}=1.15$$

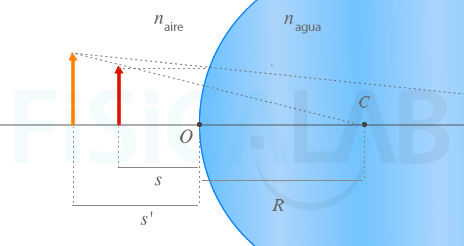
De todo esto podemos decir que la imagen del gato que ve el pez se formará a la izquierda de la pecera (es decir, en el exterior de la misma), que será mayor que el objeto original y que estará derecha ( A_L > 1 ).

Nota: Si quieres saber qué ocurriría si la pecera fuese cuadrada consulta este ejercicio.