Dioptrio esférico convexo

Datos

• Índice refracción del vídrio 1.45
• Radio de la superficie |R| = 1.6 cm = 1.6·10^-2 m
• Tamaño original de las letras: 1.8 mm = 1.8·10^-3 m
• Distancia de las letras al cilindro: 10 cm = 1·10^-1 m

Consideraciones previas

Podemos identificar los datos proporcionados con los de un sistema óptico convencional formado por un dioptrio esférico convexo (la base del cilindro) y un objeto (las letras del mapa). Así, tendríamos un esquema similar al siguiente:

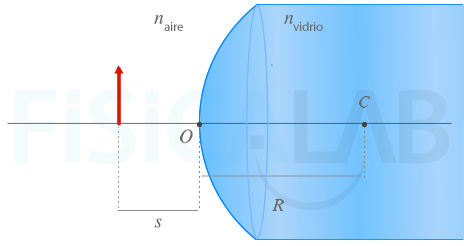
Usando el criterio DIN de signos, nos queda:

• Índice refracción dioptrio n' = 1.45
• Radio de la superficie R = 1.6 cm = 1.6·10^-2 m
• Tamaño original del objeto y = 1.8 mm = 1.8·10^-3 m
• Distancia del objeto al dioptrio s = 10 cm = 1·10^-1 m
• Índice de refracción del primer medio ( aire ) n = 1

Resolución

Comenzamos aplicando la ecuación fundamental con los datos que nos proporcionan:

$$\begin{gathered} \frac{n\text{'}}{s\text{'}}-\frac{n}{s}=\frac{n\text{'}-n}{R}\Rightarrow \frac{1.45}{s\text{'}}-\frac{1}{-1·{10}^{-1}}=\frac{1.45-1}{1.6·{10}^{-2}}\Rightarrow \frac{1.45}{s\text{'}}=\frac{0.45}{1.6·{10}^{-2}}-\frac{1}{1·{10}^{-1}}\Rightarrow \\ \Rightarrow \frac{1.45}{s\text{'}}=18.125\Rightarrow s\text{'}=0.08 m \end{gathered}$$

Por otro lado, para determinar el tamaño de las nuevas letras podemos recurrir al aumento transversal o lateral:

$$A_L=\frac{y\text{'}}{y}=\frac{n·s\text{'}}{n\text{'}·s}\Rightarrow y\text{'}=y·\frac{n·s\text{'}}{n\text{'}·s}=1.8·{10}^{-3}·\frac{1·0.08}{1.45·\left(-0.1\right)}=-0.99·{10}^{-3} m$$

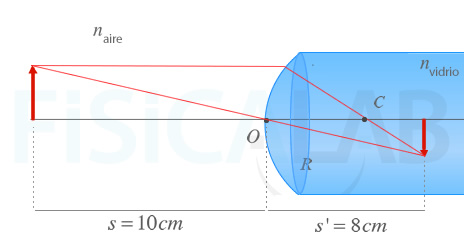
Como vemos la imagen que se forma es invertida, de menor tamaño que las letras originales y se forma a 8 cm de las mismas.