Radio dioptrio a partir de distancias focales

Datos

• Distancia focal objeto f = 10 cm = 1·10^-1 m
• Distancia focal imagen f' = -20 cm = -2·10^-1 m

Resolución

1.

En primer lugar, debemos recordar que el foco objeto es el lugar en el que habría que situar un objeto para que los rayos salgan paralelos del dioptrio una vez se refracten. Por otro lado, el foco imagen es el lugar en el que convergen los rayos que vienen del infinito (paralelos al eje óptico).

Los dioptrios convexos siempre tienen el foco objeto delante y el foco imagen detrás. Los cóncavos tienen el foco imagen deltante y el foco objeto detrás. Por tanto, nos encontramos ante el caso de un dioptrio cóncavo.

Podemos desarrollar un poco más la idea anterior. Intuitivamente se puede observar que, para que estos rayos convergan a la izquierda del dioptrio (f' es negativa), deben diverger a la derecha del mismo, y esto solo es posible en un dioptrio cóncavo (con n<n'). Algo equivalente se podría decir respecto a f. Esto se puede resumir matemáticamente diciendo que el foco imagen tendrá el mismo signo que el radio, y el  foco objeto el contrario (según criterio DIN y siempre que n'>n) . Como f' < 0 =>  R < 0 =>  dioptrio cóncavo. Las siguientes imágenes ilustran claramente la situación:

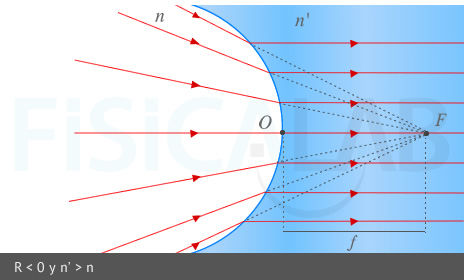
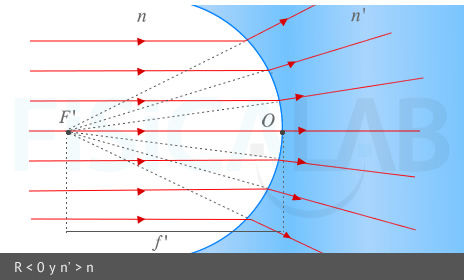
2 y 3

De las expresiones de distancia focal objeto y distancia focal imagen podemos deducir el radio y el índice de refracción pedidos, planteando el sistema de ecuaciones:

$$\left.\begin{array}{r}f=-R·\frac{n}{n\text{'}-n}\\ f\text{'}=R·\frac{n\text{'}}{n\text{'}-n}\end{array}\right\}\left.\begin{array}{r}0.1=-R·\frac{1}{n\text{'}-1}\\ -0.2=R·\frac{n\text{'}}{n\text{'}-1}\end{array}\right\}\left.\begin{array}{r}0.1·n\text{'}+R=0.1\\ -0.2·n\text{'}-R·n\text{'}=-0.2\end{array}\right\}$$ 

De la primera ecuación podemos despejar R y sustituir en la segunda:

$$\begin{gathered} R=0.1-0.1·n\text{'}\Rightarrow -0.2·n\text{'}-\left(0.1-0.1·n\text{'}\right)·n\text{'}=-0.2\Rightarrow \\ \Rightarrow 0.1·n{\text{'}}^2-0.3·n\text{'}+0.2=0\Rightarrow \left\{\begin{array}{l}n\text{'} =\hspace{0.17em}2\\ \xcancel{n\text{'} =\hspace{0.17em}1}\end{array}\right. \end{gathered}$$

Donde hemos despreciado n'=1 por implicar que no habría cambio de medio.

Por otro lado, sustituyendo en la primera de las ecuaciones:

$$R=0.1-0.1·n\text{'}\Rightarrow R\hspace{0.17em}=0.1-0.1·2=-0.1 m$$

Finalmente, recordarte que si conoces las dos expresiones siguientes, quizá te resulte más inmediato resolver este apartado, pero ten presente que, como hemos visto, bastan las expresiones de las distancias focales. 

Sumando la expresión de f y f' obtenemos:

$$f+f\text{'}=R$$

Diviediendo f y f' obtenemos: 

$$\frac{f}{f\text{'}}=-\frac{n}{n\text{'}}$$