Proyección en un punto de imagen de espejo esférico

Datos

• Altura bombilla (objeto): y = 3 cm = 0.3 m
• Distancia objeto - imagen: 4 m = 400 cm
• Espejo cóncavo de radio |R| = 90 cm = 0.9 m

Consideraciones previas

Observa que hemos indicado el radio valor absoluto, siguiendo el criterio DIN sabemos que, para espejos cóncavos R<0 => R = -0.9 m . Por otro lado, la siguiente imagen ilustra la situación:

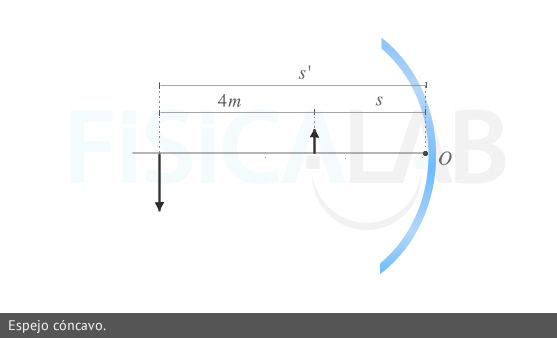
Observa que hemos dibujado la imagen invertida. Aunque no es relevante que lo sepas a priori, piensa que el aumento transversal, $A_L=\frac{y\text{'}}{y}=-\frac{s\text{'}}{s}$ , cuando s y s' son negativas es negativo, y por tanto la imagen se invierte.

Resolución

Comenzamos obteniendo el valor de la distancia focal del espejo:

$$f=\frac{R}{2}=-0.45 m$$ 

Por otro lado, s y s' son negativas, así: 

$$\left|s\text{'}-s\right|=4\Rightarrow s-s\text{'}=4$$

Así, aplicando la ecuación fundamental y sustituyendo s' = s-4 :

$$\begin{gathered} \frac{1}{s}+\frac{1}{s\text{'}}=\frac{1}{f}\Rightarrow \frac{1}{s}+\frac{1}{s-4}=\frac{1}{f}\Rightarrow \frac{s+s-4}{s·\left(s-4\right)}=\frac{1}{f}\Rightarrow \\ \Rightarrow 2·s·f-4·f=-4·s+s^2\Rightarrow s^2-3.1·s-1.8=0\Rightarrow \left\{\begin{array}{l}{s}_1=\cancel{3.6 m}\\ s_2=-0.5 m\end{array}\right. \end{gathered}$$

Es decir, situaremos la bombilla a 0.5 m del espejo, a su izquierda. Observa que hemos tachado la solución positiva ya que implicaría situar el objeto a la derecha del espejo, comportándose en realidad como un espejo convexo y creando una imagen virtual, no real, en el punto deseado.