Lente para proyectar imagen en pantalla

Datos

• Distancia del objeto a la pantalla |s| + |s'| = 8 m
• Tamaño de la imagen: y' = -2·y (imagen invertida)

Resolución

Para que la lente forme la imagen del objeto en la pantalla, esta debe ser una imagen real. Recuerda que sólo las lentes convergentes son capaces de producir imágenes reales. Puedes deducir esta afirmación a partir de la ecuación de Gauss para las lentes delgadas:

$$\frac{1}{s\text{'}}-\frac{1}{s}=\frac{1}{f\text{'}}\Rightarrow \frac{1}{s\text{'}}=\frac{1}{f\text{'}}+\frac{1}{s}$$

Para que la imagen sea real, debe situarse a la derecha de la lente (s'>0). En la expresión anterior puedes observar que esto sólo ocurre cuando 1/s' > 0, pero para que esto pase, dado que 1/s < 0, 1/f' debe ser mayor que cero. Esto sólo pasa en las lentes convergentes.

Por otro lado, a partir de la expresión del aumento transversal... 

$$A_L=\frac{y\text{'}}{y}=\frac{s\text{'}}{s}\Rightarrow \frac{-2·y}{y}=\frac{s\text{'}}{s}\Rightarrow s\text{'}=-2·s$$

Por otro lado, sabemos que la distancia objeto pantalla es de 8 metros y que situamos el objeto a la izquierda, es decir, s < 0 . Recordando que |s| = -s si s<0 nos queda:

$$\begin{gathered} \left|s\right|+\left|s\text{'}\right|=8\Rightarrow -s+\left(-2·s\right)=8\Rightarrow s=-\frac{8}{3} m; \\ s\text{'}=-2·s=\frac{16}{3} m; \end{gathered}$$

Sabemos dónde colocar el objeto, ahora vamos a determinar la distancia focal que debe tener la lente. Volvemos a la ecuación de Gauss de las lentes delgadas:

$$\frac{1}{s\text{'}}-\frac{1}{s}=\frac{1}{f\text{'}}\Rightarrow \frac{3}{16}-\left(-\frac{3}{8}\right)=\frac{1}{f\text{'}}\Rightarrow \frac{9}{16}=\frac{1}{f\text{'}}\Rightarrow f\text{'}=16/9 =\hspace{0.17em}1.77 m$$

La siguiente imagen ilustra la situación en que quedarían objeto, lente, pantalla e imagen:

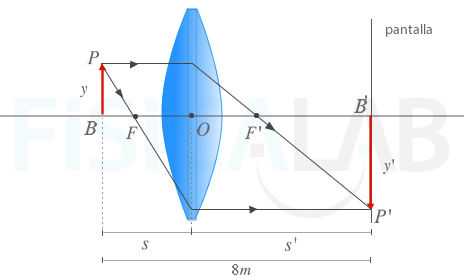
"¿Existe otra posición para dicha lente que también consiga enfocar el objeto en la pantalla?"

De existir dicha posición debe cumplir las ecuaciones:

$$\begin{gathered} \frac{1}{s\text{'}}-\frac{1}{s}=\frac{1}{f\text{'}}; \\ \left|s\right|+\left|s\text{'}\right|=8; \end{gathered}$$

Dado que la segunda ecuación está escrita con valores absolutos, comenzaremos por quitarlos:

$$\left|s\right|+\left|s\text{'}\right|=8\Rightarrow \left\{\begin{array}{c}\begin{array}{c}s+s\text{'}=8 si s>0 y s\text{'}>0\\ \cancel{s-s\text{'}=8 si s>0 y s\text{'} <0}\\ \boxed{-s + s\text{'} =\hspace{0.17em}8 si s<0 y s\text{'}>0}\\ \cancel{-s -s\text{'} =\hspace{0.17em}8 si s<0 y s\text{'}<0}\end{array}\end{array}\right.$$

Observa que hemos tachado las expresiones que tienen s'<0 o s>0, ya que implican imagen virtual o el objeto a la izquierda de la lente. Ahora ya estamos en disposición de usar las dos ecuaciones para buscar, si existe, otra disposición para la lente que forme imágenes reales en la pantalla:

$$\begin{gathered} -s + s\text{'} =\hspace{0.17em}8\Rightarrow s\text{'}=8+s \left[1\right] \\ \frac{1}{s\text{'}}-\frac{1}{s}=\frac{1}{f\text{'}}\underset{\left[1\right]}{\Rightarrow }\frac{1}{8+s}-\frac{1}{s}=\frac{1}{f\text{'}}\Rightarrow \frac{s-\left(8+s\right)}{s·\left(8+s\right)}=\frac{1}{f\text{'}}\Rightarrow \boxed{s^2+8·s+8·f\text{'}=0} \end{gathered}$$

Resolviendo la ecuación nos queda:

$$\begin{gathered} \boxed{s_1=-5.33\Rightarrow s{\text{'}}_1=2.66} \\ {s}_2=-2.66\Rightarrow s{\text{'}}_2=5.33 \end{gathered}$$

La segunda de las soluciones, s₂, s'₂, corresponde al apartado anterior. En relación a la primera, observa que el tamaño de la imagen, en este caso, sería:

$$A_L=\frac{y\text{'}}{y}=\frac{s\text{'}}{s}=\frac{2.66}{-5.33}=-\frac{1}{2}\Rightarrow y\text{'}=-y/2$$

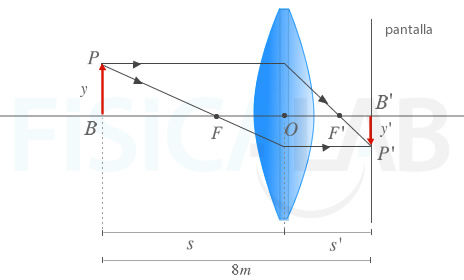
Es decir, se trata de una imagen real, que se proyectaría en la pantalla, pero esta vez el tamaño sería menor que el del objeto original. La siguiente imagen ilustra la nueva situación