Imágenes formadas por dos lentes convergentes separadas

Datos

• Distancia entre lentes d = 60 cm
• Distancia del objeto a la primera lente |s₁| = 50 cm
• Altura del objeto y = 4 cm
• Distancia focal imagen de las lentes f'₁ = f'₂ = 20 cm

Consideraciones previas

Se trata de un sistema formado por dos lentes. La siguiente imagen describe la situación inicial:

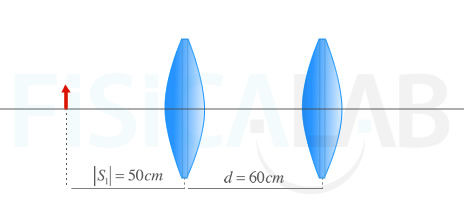
Comenzaremos estudiando la primera lente como si la segunda no estuviera y posteriormente consideraremos la imagen de la primera lente el objeto de la segunda lente. La imagen producida por la segunda lente es la imagen del sistema que nos piden.

Por otro lado:

• Como es habitual, seguiremos el criterio DIN de signos para el estudio de cada lente
• Utilizaremos por comodidad el cm como unidad de distancias, a pesar de que la unidad del Sistema Internacional es el metro

• Partiendo de la ecuación fundamental de las lentes delgadas, podemos llegar a la ecuación gaussiana de las lentes delgadas, asumiendo que las lentes se encuentran en el aire ( n=1 ). Dicha expresión nos será particularmente útil:

  $$\begin{gathered} \frac{n}{s\text{'}}-\frac{n}{s}=\left(n\text{'}-n\right)·\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\stackrel{\begin{array}{c}s=\infty \\ s\text{'}=f\text{'}\end{array}}{\Rightarrow }\frac{n}{f\text{'}}=\left(n\text{'}-n\right)·\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\Rightarrow \\ \Rightarrow \frac{n}{s\text{'}}-\frac{n}{s}=\frac{n}{f\text{'}}\stackrel{n=1}{\Rightarrow }\boxed{\frac{1}{s\text{'}}-\frac{1}{s}=\frac{1}{f\text{'}}} \end{gathered}$$

Resolución

Dado que el objeto se encuentra a la izquierda de la primera lente, s₁ = -50 cm, con lo que s'₁:

$$\frac{1}{s{\text{'}}_1}-\frac{1}{s_1}=\frac{1}{f\text{'}}\Rightarrow \frac{1}{s{\text{'}}_1}-\frac{1}{-50}=\frac{1}{20}\Rightarrow s{\text{'}}_1=33.3 cm$$

Es decir, la imagen de la primera lente se forma 33.3 cm a la derecha de la primera lente. Dado que esta está separada 60 cm de la segunda, s₂=60-33.3 = 26.66 cm. Aplicando ahora la ecuación de Gauss a la segunda lente, y teniendo en cuenta que s₂ es negativa al estar a la izquierda de la misma, nos queda:

$$\frac{1}{s{\text{'}}_2}-\frac{1}{s_2}=\frac{1}{f\text{'}}\Rightarrow \frac{1}{s{\text{'}}_2}-\frac{1}{-26.66}=\frac{1}{20}\Rightarrow s{\text{'}}_2=80 cm$$

Por tanto, el objeto se forma 80 cm a la derecha de la segunda lente. En cuanto a su tamaño, debemos calcular el aumento lateral de cada lente:

$$\begin{gathered} A_{L_1}=\frac{s{\text{'}}_1}{s_1}=\frac{33.3}{-50}=-0.66; \\ {A}_{L_2}=\frac{s{\text{'}}_2}{s_2}=\frac{80}{-26.66}=-3; \end{gathered}$$

El aumento lateral total del sistema es el producto de ambos, y a partir de ahí puedo calcular el tamaño final y' de la imagen tras atravesar todo el sistema:

$$A_{L_T}=\frac{y\text{'}}{y}=A_{L_1}·A_{L_2}=-0.66·\left(-3\right)=1.98\Rightarrow y\text{'}=A_{L_T}·y=1.98·4=7.92cm$$

Es decir, la imagen final es derecha y de mayor tamaño que la original.