Desfase en m.a.s. a partir de gráficas
Enunciado
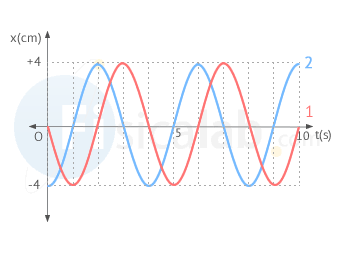
Determina las ecuaciones de las gráficas de la figura. Determina también el desfase entre ambos movimientos.
Solución
Datos
Los datos del problema están implicitos en la gráfica.
Consideraciones previas
Existen dos expresiones posibles para la ecuación de un movimiento armónico simple. En funcion del seno o en función del coseno. Para determinar el desfase lo mejor es expresar las dos de igual manera.
Vamos a utilizar el coseno. Recordemos la representación de la función

Resolución
A partir de la gráfica podemos obtener las magnitudes de cada movimiento:
- Amplitud: A = 4 cm
- Periodo: T = 4 s
- Frecuencia f= 1/T = 0.25 Hz
- Pulsación o frecuencia angular ω : ω = 2·π·f = 0.5·π rad/s
La expresión será de la forma.
- 1:
- 2:
Nos queda determinar la fase inicial de cada una. Lo hacemos a partir del valor en t = 0.
Finalmente el desfase se puede calcular como la diferencia de fase entre una señal y otra en cualquier instante. Para simplificar los cálculos tomamos el instante t = 0
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
