Funciones Trigonométricas
En el tema dedicado a la trigonometría veíamos la definición de las distintas razones trigonométricas. Ya debes estar familiarizado con el seno, el coseno y la tangente de un ángulo, por ejemplo. También deberían resultarte familiares a estas alturas las razones inversas: la cosecante, la secante y la cotangente. Pues bien, una función trigonométrica no es más que una función en la que la variable independiente, normalmente llamada x, se encuentra afectada por una de estas operaciones.
A las funciones trigonométricas también se las denomina frecuentemente funciones circulares. Una de sus principales características es que son periódicas.
En este apartado vamos a hacer un análisis detallado de todas ellas a través de los siguientes puntos:
- Definición y algunos ejemplos
- Gráficas
- Dominio
- Imagen o recorrido
- Periodicidad
- Continuidad y derivabilidad
- Asíntotas y ramas
- Simetría
- Puntos de corte con los ejes y signo
- Monotonía y extremos
- Curvatura y puntos de inflexión
- Representación
- Fenómenos reales descritos
¿Empezamos?
Definición
Estudiaremos las propiedades de las funciones trigonométricas, tanto de las razones directas, como de las razones inversas o recíprocas, que en su forma más simple, son:
| Razones directas | Razones inversas |
| Función seno f(x)=sin(x) |
Función cosecante |
| Función coseno f(x)=cos(x) |
Función secante |
| Función tangente f(x)=tan(x)=sin(x)/cos(x) |
Función cotangente |
Todas ellas asocian a cada ángulo x (normalmente expresado en radianes), el valor de la razón correspondiente.
Las funciones cosecante, secante y arcotangente son inversas respecto al producto (inverso multiplicativo o recíproco) de las funciones seno, coseno y tangente. En algunos textos verás que llaman funciones trigonométricas inversas al arcoseno, arcocoseno y arcotangente. Estas últimas son realmente inversas respecto a la composición. Para evitar confusiones, en caso de ambigüedad, nosotros llamaremos a estas últimas funciones arco, de acuerdo a la norma ISO 80000-2.
Algunos ejemplos
- f(x)=3·sin(x)
- f(x)=cos(3x)
- f(x)=2·tan(5x+π/3)
En el epígrafe dedicado a la representación gráfica, más abajo, veremos en detalle como se modifican las funciones más simples al aplicar las transformaciones (desplazamientos y escalados) señalados en negrita.
Un breve paréntesis: ¿qué son exactamente las funciones sinusoidales?
De entre todas las funciones trigonométricas, merecen especial atención las conocidas como sinusoidales.
De manera general, hablamos de funciones sinusoidales o sinusoides cuando nos referimos a aquellas funciones trigonométricas que tienen la forma de la función seno, es decir:
Donde podemos encontrar los siguientes parámetros:
- A : Ampitud de la función. Se trata del valor máximo que tomará la misma. En el caso de que la función represente algún fenómeno físico, como por ejemplo la elongación de un muelle, las unidades de A deben coincidir con las unidades de la magnitud representada por f(x)
- B : Este parámetro controla la frecuencia (y por consiguiente el periodo), de la función. Dado que lo que hay dentro del seno (o del coseno) debe ser un ángulo (cuya unidad de medida más habitual son los radianes o los grados), las unidades de B deben ser tales que, al multiplicarlas por las unidades de la variable independiente x resulten en radianes o grados. Por ejemplo es habitual que la variable x represente el tiempo t, medido en segundos siendo entonces B conocida como frecuencia angular, y representada mediante ω, y con unidad de medida rad/s. La relación entre B y el periodo, normalmente designado por T, es T=2π/B
- C : Este parámetro controla la fase inicial. Se denomina fase al argumento del seno (o del coseno), y por tanto B es la fase cuando x=0. También se mide utilizando unidades angulares, como los radianes, y es habitualmente representada en física mediante φ0
Normalmente utilizamos estas funciones para modelar fenómenos reales tales como el comportamiento de ondas armonicas o la corriente eléctrica alterna. Te invitamos a que visites el apartado sobre el movimiento armónico simple para encontrar una definición más formal de tales conceptos.
En algunos textos verás que cuando utilizamos la expresión analítica del coseno se habla de cosinusoides.
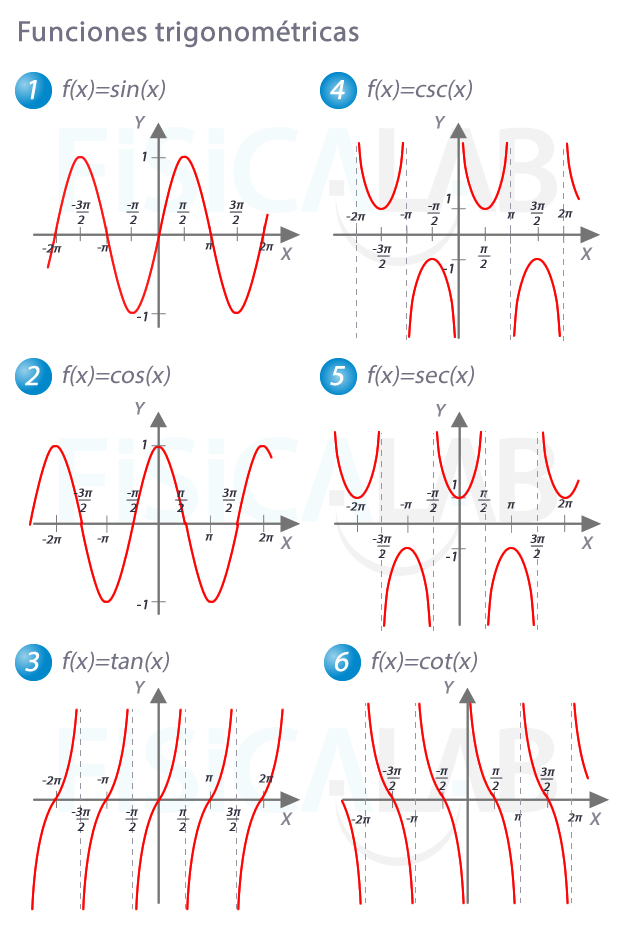
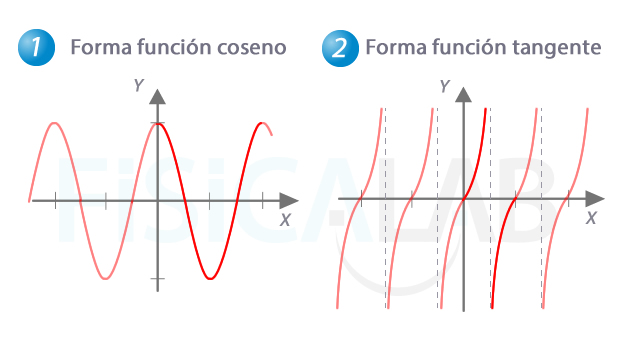
Gráficas
Las funciones seno y coseno están acotadas, ya que |sin(x)|≤1 y |cos(x)|≤1. El resto no, ya que, como veremos más abajo, presentan asíntotas.
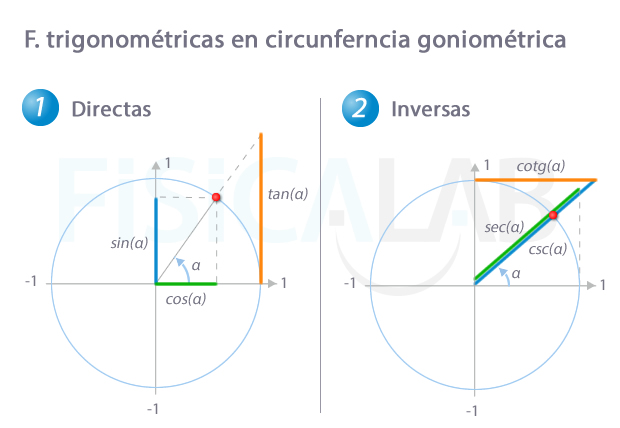
Interpretación geométrica
Para visuaizar como se pueden generar las funciones trigonométricas es habitual pensar en un punto que se desplaza sobre la circunferencia goniométrica a una velocidad constante. Las longitudes a lo largo del tiempo de las proyecciones con los ejes o con otros elementos de la circunferencia daría lugar a las funciones trigonométricas estudiadas. Observa la siguiente imagen.
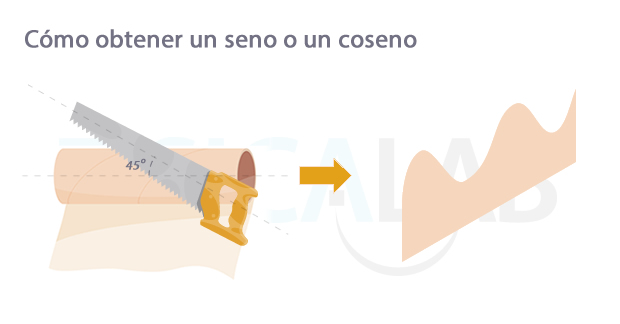
Otra forma de plasmar una sinusoide es a través de un rollo de servilleta.
Transformaciones y parámetros
A partir de las gráficas anteriores, y aplicando las transformaciones de funciones que ya conoces, es muy fácil representar funciones trigonométricas más complejas. Veamos algunos ejemplos.
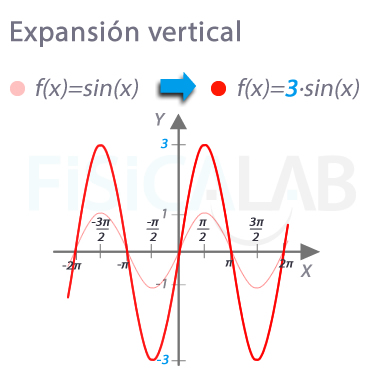
Expansión/contracción en eje y
Si multiplicamos la función trigonométrica original por un valor k (3 en este caso), estamos cambiando su escalado en el eje y. Observa en la imagen como el efecto es el de una expansión. Si el valor de k estuviese entre 0 y 1 el efecto sería el de una contracción en el eje y.
En el caso concreto de la función seno (y también coseno), lo que cambia es la amplitud de la misma.
Puedes utilizar la simulación para comprobar que la expansión vertical correspondería a un cambio en el radio de la circunferencia utilizada como referencia (originalmente la goniométrica).
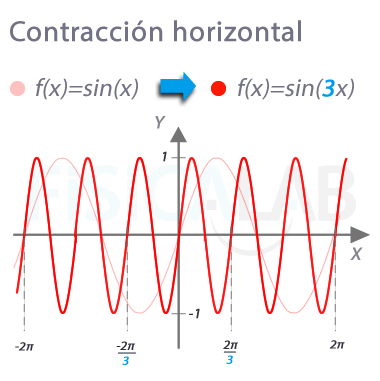
Contracción/expansión en eje x
Si multiplicamos la variable independiente (x en este caso) por un valor k (3 en este caso), estamos cambiando su escalado en el eje x. Observa en la imagen como el efecto es el de una contracción. Si el valor de k estuviese entre 0 y 1 el efecto sería el de una expansión en el eje x.
En el caso concreto de la función seno (y también coseno), lo que cambia es la frecuencia de la misma (y por tanto su periodo). Así, observa la función original en rojo claro, que se repite cada 2π, en cambio la función transformada, en rojo intenso se repite cada 2π/3.
Puedes utilizar la simulación para comprobar que la contracción horizontal correspondería a un cambio en la velocidad angular de giro sobre la circunferencia goniométrica.
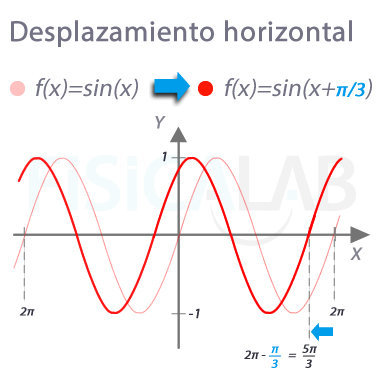
Desplazamiento en eje x
Si sumamos al argumento del seno un valor k (π/3 en este caso), estamos "moviéndo" la función en el eje x. Se produciría un desplazamiento hacia la izquierda si k>0, y hacia la derecha si k<0.
En el caso concreto de la función seno (y también coseno), lo que cambia es la fase inicial de la misma, es decir, el valor de la función para x=0.
Puedes utilizar la simulación enlazada para comprobar que el desplazamiento horizontal corresponde con un cambio en el punto inicial sobre el que nos situamos en la circunferencia goniométrica.
Dominio
El dominio, como ya sabes, es el conjunto de valores que puede tomar la variable independiente x. Las funciones f(x)=sin(x) y f(x)=cos(x) tienen por dominio el conjunto de los reales ℝ. Dado que el resto de razones se pueden obtener como cocientes a partir de estas dos, en el cálculo de su dominio deberemos quitar los valores que anulen el denominador. Te resumimos esta idea en la siguiente tabla.
| Función | Dominio |
| Función seno f(x)=sin(x) |
Domf=ℝ |
| Función coseno f(x)=cos(x) |
Domf=ℝ |
| Función tangente f(x)=tan(x)=sin(x)/cos(x) |
|
| Función cosecante f(x)=csc(x)=1/sin(x) |
|
| Función secante f(x)=sec(x)=1/cos(x) |
|
| Función cotangente f(x)=tan(x)=1/tan(x)=cos(x)/sin(x) |
Aclaraciones
Puede que te estés preguntando qué significan esos "jeroglíficos" que corresponden al dominio de las 4 últimas funciones. No te dejes intimidar. Vamos a traducir desde el lenguaje natural (castellano en nuestro caso), al matemático:
En el apartado específico dedicado al estudio del dominio de funciones puedes encontrar más ejemplos para profundizar sobre el dominio de funciones trigonométricas.
Ahora que ya sabes (o has recordado) como expresar estas dos ideas en lenguage matemático... ¿seguimos?
Recorrido
El recorrido, como probablemente ya has estudiado, es el conjunto de valores que toma la función en sí, esto es, el conjunto de valores que toma la variable dependiente y. Cuando definíamos las razones trigonométricas habíamos visto por qué el valor del seno y del coseno siempre eran menores o iguales que 1. De ahí que la imagen de f(x)=sin(x) y de f(x)=cos(x) sea precisamente [-1, 1]. Observando las gráficas que te hemos presentado en el epígrafe anterior puedes comprobar que...
| Función | Recorrido |
| Función seno f(x)=sin(x) |
Recf=[-1, 1] |
| Función coseno f(x)=cos(x) |
Recf=[-1, 1] |
| Función tangente f(x)=tan(x)=sin(x)/cos(x) |
Recf=ℝ |
| Función cosecante f(x)=csc(x)=1/sin(x) |
|
| Función secante f(x)=sec(x)=1/cos(x) |
|
| Función cotangente f(x)=cot(x)=1/tan(x)=cos(x)/sin(x) |
Recf=ℝ |
Observa que el recorrido de las funciones cosecante y secante es el "complementario" del de las funciones seno y coseno correspondientes.
Aclaraciones
Queremos seguir ayudándote a descifrar "jeroglíficos" así que vamos a ello...
Efectivamente, dado que la cosecante y la secante, por definición, resultan en 1/(algo que oscila entre -1 y 1), su valor siempre será, en valor absoluto, mayor o igual que 1.
Periodicidad
Intuitivamente, decimos que una función cualquiera es periódica cuando repite su forma cada cierto intervalo de su variable independiente x llamado periodo (normalmente representado por T ). Esto es, si f(x)=f(x+T) para cualquier x∈Domf.
Las funciones trigonométricas son periódicas.
Los periodos de las funciones trigonométricas más sencillas, quedan recogidos en la siguiente tabla:
| Función | Periodo |
| f(x)=sin(x) f(x)=cos(x) f(x)=csc(x) f(x)=sec(x) |
T=2π |
| f(x)=tan(x) f(x)=cot(x) |
T=π |
Revisa las gráficas en el epígrafe anterior para verificar estos periodos.
Transformaciones y periodicidad
La periodiciad de las funciones trigonométricas arroja algunos resultados curiosos cuando aplicamos transformaciones. Puedes jugar con la simulación de funciones trigonométricas para observar los efectos que describirmos a continuación:
-
¿Qué ocurre si en lugar de f(x)=sin(x) tenemos, por ejemplo, f(x)=sin(a·x) siendo a un número real cualquiera? El periodo se reduce (contracción) o se amplía (expansión)
- f(x)=cos(x) ⇒ T=2π
- f(x)=cos(3x) ⇒ T=2π/3
- f(x)=cos(0.5x) ⇒ T=2π/0.5=4π
- f(x)=cos(x) ⇒ T=2π
Si aplicamos un desplazamiento horizontal múltiplo del periodo las funciones pueden ser indistinguibles:
sin(x)=sin(x+2π)
cos(3x)=cos(3(x-2π/3))
De todo lo anterior se deduce que cuando, en lugar de f(x)=sin(x), f(x)=cos(x), f(x)=csc(x) ó f(x)=sec(x), tenemos f(x)=sin(B·x), f(x)=cos(B·x), f(x)=csc(B·x) ó f(x)=sec(B·x), el periodo fundamental pasa de T=2π a T=2π/B.
En caso de que, en lugar de f(x)=tan(x) ó f(x)=cot(x), tengamos f(x)=tan(B·x) ó f(x)=cot(B·x), el periodo fundamental pasa de T=π a T=π/B.
En Física, al estudiar las ondas, el parámetro B, estrechamente relacionado con el periodo T en las sinusoides, es conocido como frecuencia angular. Visita el apartado vinculado para profundizar sobre ello.
Continuidad y derivabilidad
Las funciones trigonométricas son continuas y derivables en todo su dominio.
Esto significa que:
| Función | Es continua y derivable en... |
| f(x)=sin(x) f(x)=cos(x) |
ℝ |
| f(x)=tan(x) f(x)=sec(x) |
|
| f(x)=csc(x) f(x)=cot(x) |
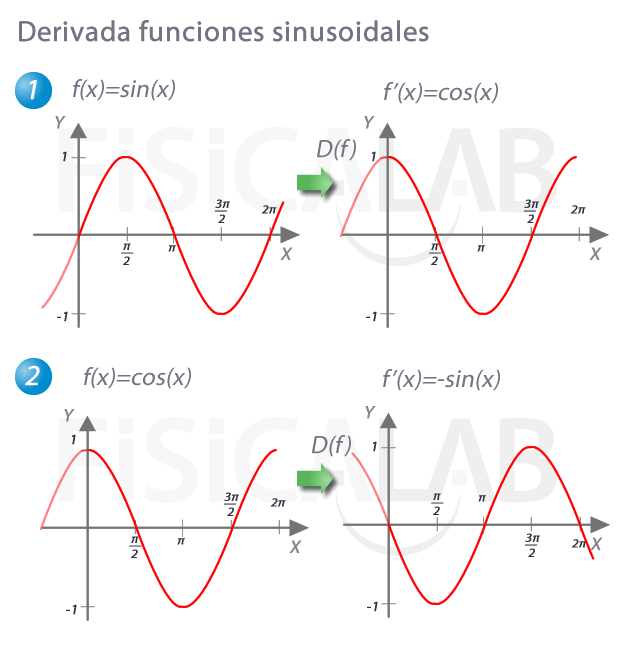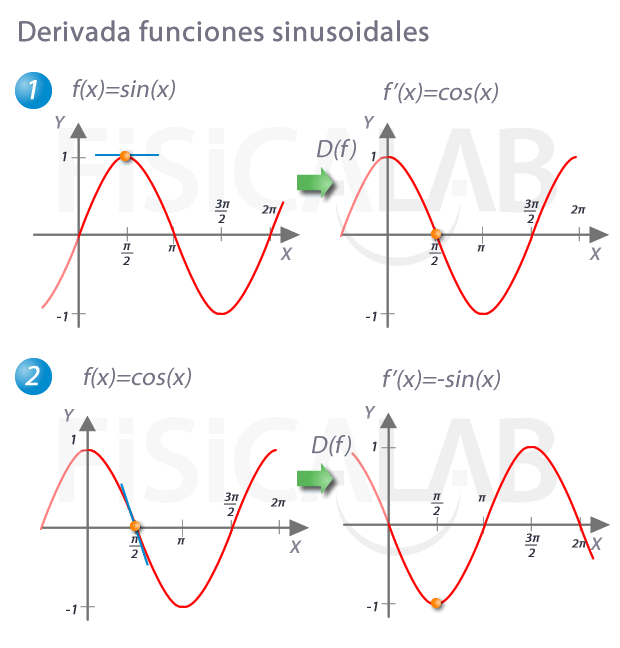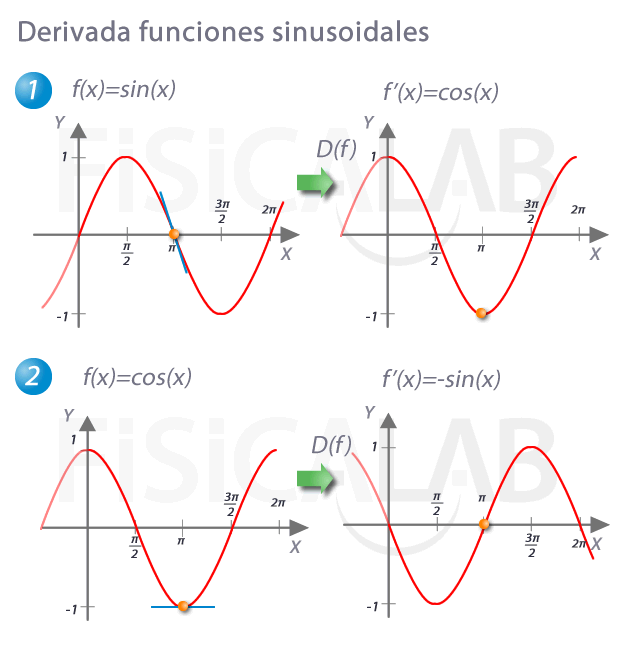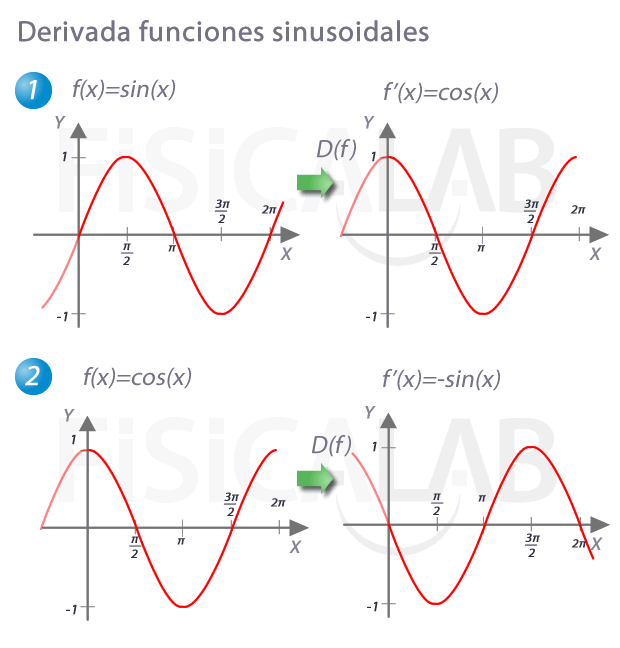
Por otro lado, recuerda que la función derivada de otra nos indica como evoluciona la pendiente de la recta tangente en cada punto de la función original. Así, observa las relaciones:
Las derivadas del resto de funciones trigonométricas se obtienen fácilmente a partir de estas y aplicando las propiedades de las derivadas.
Asíntotas y ramas
Al ser periódicas, las funciones trigonométricas no poseen ramas parabólicas.
En cambio, observando las gráficas podemos ver que poseen asíntotas verticales:
- f(x)=csc(x) en
- f(x)=sec(x) en
- f(x)=tan(x) en
- f(x)=cot(x) en
Observa que estas discontinuidades asintóticas son periódicas, y aparecen en aquellos valores de x en los que se anularía el sin(x) o el cos(x) que, por definición, se encuentre en el denominador. Entender esto nos permite buscar las asíntotas verticales en funciones más complejas.
Ejemplo
Simetría
Las funciones trigonométricas más simpes son simétricas, según se recoge en la siguiente tabla.
| Simetría impar f(-x)=-f(x) |
f(x)=sin(x) f(x)=tan(x) f(x)=csc(x) f(x)=cot(x) |
| Simetría par f(x)=f(-x) |
f(x)=cos(x) f(x)=sec(x) |
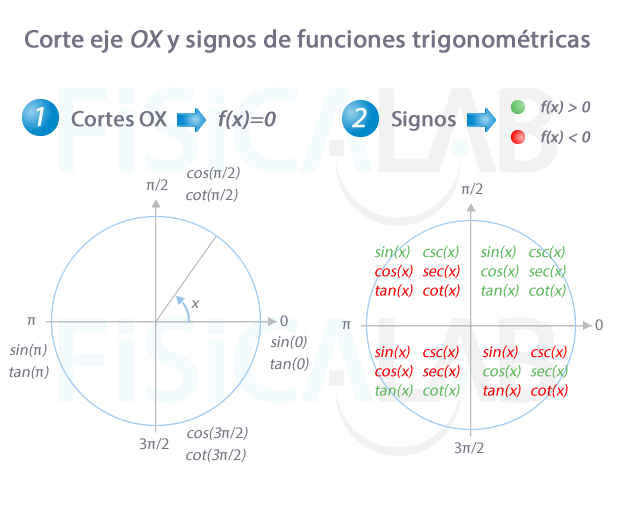
Corte con los ejes y signo
En la siguiente tabla quedan recogidos los puntos de corte, tanto con eje x como con el eje y.
| Función | Cortes OX | Corte OY |
| sin(x), tan(x) | (0,0) | |
| cos(x) | (0,1) | |
| csc(x) | No hay cortes | No hay corte |
| sec(x) | No hay cortes | (0, 1) |
| cot(x) | No hay corte |
* Con k∈ℤ.
Monotonía y extremos
Para estudiar la monotonía de las funciones trigonométricas, así como sus máximos y mínimos, podemos seguir el procedimiento habitual. Dado que se trata de un procedimiento largo, te resumimos aquí los resultados, que puedes comprobar tú mismo observano las gráficas:
| Función | Crece* | Derece* | Máximos* | Mínimos* |
| f(x)=sin(x) | ||||
| f(x)=cos(x) | ||||
| f(x)=tan(x) | Todo su dominio, esto es, |
La función no es decreciente en ningún intervalo. | La función no presenta máximos | La función no presenta mínimos |
| f(x)=csc(x) | ||||
| f(x)=sec(x) | ||||
| f(x)=cot(x) | La función no es creciente en ningún intervalo. | Todo su dominio, esto es, |
La función no presenta máximos | La función no presenta mínimos |
* Con k∈ℤ.
Es posible que en otros textos veas estos intervalos, y cualesquiera otros, relativos a las funciones trigonométricas, expresados de forma diferente. Esto es debido a la periodicidad de este tipo de funciones.
Curvatura y puntos de inflexión
Al igual que sucede con el crecimiento y el decrecimiento, para estudiar la curvatura de las funciones trigonométricas, así como sus puntos de inflexión (esto es, los puntos en los que la función pasa de cóncava a convexa o viceversa), podemos seguir el procedimiento habitual. Igualmente, te resumimos aquí los resultados obtenidos:
| Función | Cónvava | Convexa | Puntos de inflexión |
| f(x)=sin(x) | |||
| f(x)=cos(x) | |||
| f(x)=tan(x) | |||
| f(x)=csc(x) | No hay punto de inflexión, ya que el cambio de curvatura se produce en x=π + 2kπ, que no pertenece al dominio | ||
| f(x)=sec(x) | No hay puntos de inflexión, ya que los cambios de curvatura se produce en x=π/2 y en x=3π/2 +2kπ, que no pertenecen al dominio | ||
| f(x)=cot(x) |
* Con k∈ℤ.
Consejos de representación
Aunque existe un método genérico para la representación de funciones cualesquiera, en el caso de las trigonométricas podemos hacer uso de sus características que hemos analizado para simplificar el proceso. Te recomendamos que sigas los siguientes pasos:
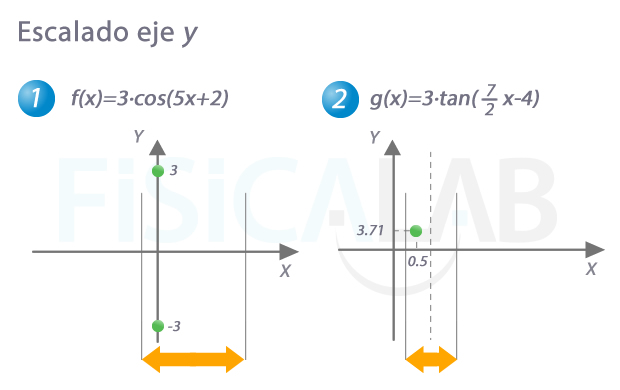
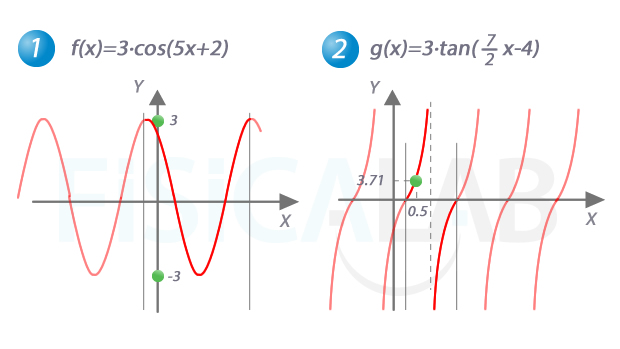
Debemos tener en mente la forma de la función que estamos representando, que ya hemos estudiado en el epígrafe gráficas. Como ejemplo vamos a hacer una representación de las funciones f(x)=3·cos(5x+2) y g(x)=3·tan((7/2)x-4)
Vamos a representar un periodo, y a replicarlo. Para ello comenzamos, si es necesario, por sacar factor común de la fase el coeficiente que acompaña a la x. Así:
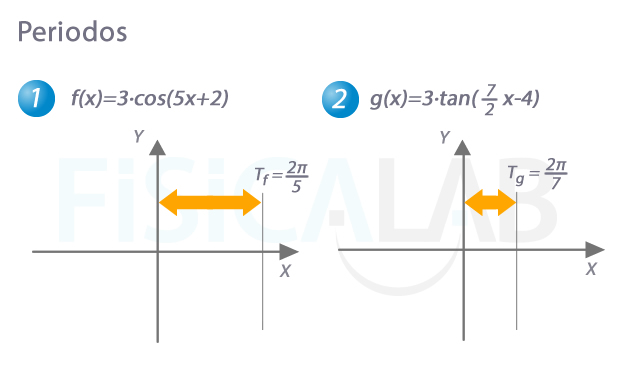
Seguidamente, calculamos dicho periodo. Si llamamos B al factor en negrita, el periodo T será:
- T=2π/B en las funciones seno, coseno, cosecante y secante
- La mitad, esto es T=π/B en las funciones tangente y cotangente
Por tanto,
Representamos dicho intervalo como periodo fundamental, para establecer la escala del eje x
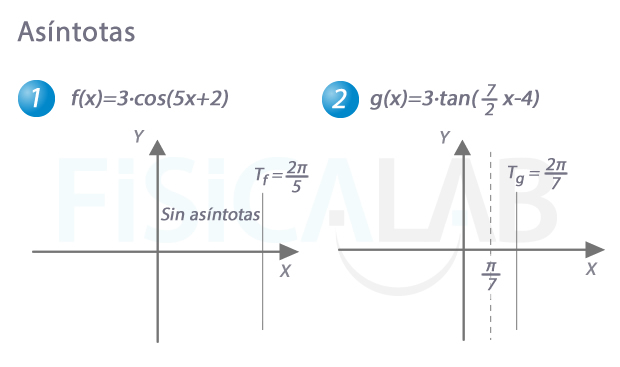
Marcamos, si las hubiera, las asíntotas verticales que caen en el periodo representado. Seguiremos como referencia la siguiente tabla:
Función Posición asíntota/s vertical tan(x) T/2 csc(x) 0 y T/2 sec(x) T/4 y 3T/4 cot(x) 0 En nuestro caso, marcamos la asíntota en T/2=π/7
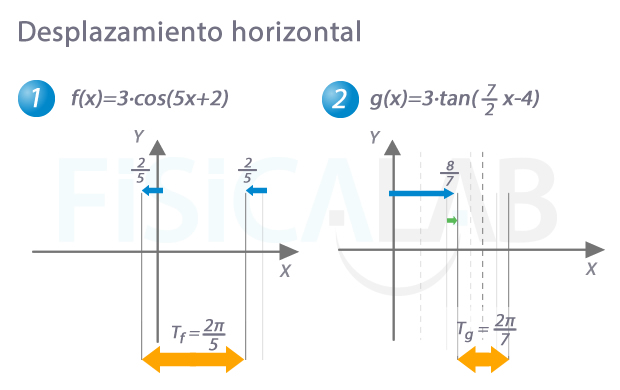
Desplazamos el periodo representado, si fuera necesario, según el valor que sume o reste a x. Recuerda que los desplazamientos en el eje x se hacen en el sentido contrario al que intuitivamente nos marcaría el signo (con - tenemos que desplazar a la derecha, con + tenemos que desplazar a la izquierda). Por otro lado, recuerda también que, dado que las funciones trigonométricas son periódicas, un desplazamiento superior al periodo es equivalente a un desplazamiento en el periodo fundamental
Establecemos un punto de referencia, para el escalado del eje y. En el caso de las funciones seno, coseno, cosecante y secante, este puede ser el valor del coeficiente que acompaña a la función (la amplitud del seno o del coseno). En el caso de la tangente y la cotangente simplemente asigna un valor a la x para ver el valor de la y y utilizarlo como referencia
Finalmente, pintamos la forma de la función en el periodo indicado, y replicamos
Una vez representada, ayúdate de este simulador para comprobar que el resultado era correcto.
Aplicaciones en ciencias
Las funciones trigonométricas son ampliamente utilizadas en física química e ingeniería. Veamos algunos ejemplos.
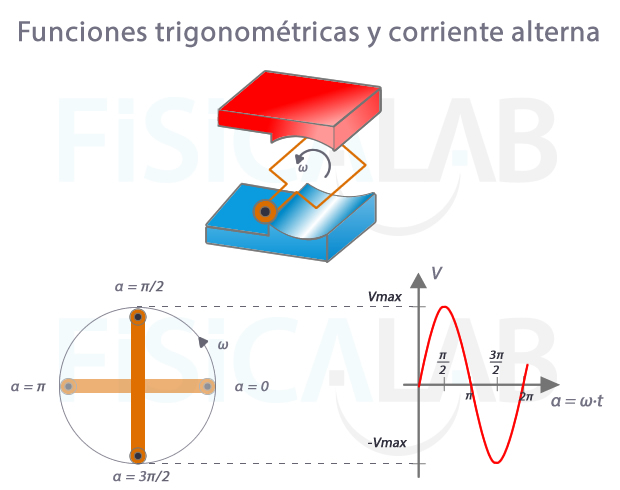
Corriente alterna (C.A.). Cuando hacemos girar una espira en el seno de un campo magnético según un m.c.u., el flujo magnético que atraviesa la espira varía. Esto provoca una corriente inducida en la espira que tiene la forma de una función sinusoidal.
Momento de fuerza. El momento de una fuerza es una magnitud que se define como un producto vectorial. En este caso concreto significa que, para una fuerza y una distancia al punto de giro determinadas, el valor del momento varía con el ángulo aplicado según la función seno.
El sonido. El sonido es una onda de presión, que puede ser descrita como una suma de funciones sinusoidales. Esto se debe a que cualquier función puede ser descrita mediante la descomposición en series de Fourier (esto es justamente eso, una suma de sinusoides de distinta frecuencia y amplitud). El análisis y síntesis de Fourier es fundamental para el tratamiento de señales de cualquier tipo. En concreto, si queremos producir el sonido de un piano de manera electrónica, por ejemplo, podemos generar una suma de funciones senos y cosenos que "simule" el tono y timbre original de la nota buscada del piano.
Espectrometría. Se trata de una técnica que permite analizar sustancias, encontrando su composición a partir del análisis de ondas que inciden sobre la misma. De ahí que para su desarrollo fue fundamental el manejo de funciones trigonométricas
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.