Segunda Ley de Newton
El físico, matemático y astrónomo Inglés Sir Isaac Newton (1642-1727), basándose en los estudios de Galileo y Descartes, publicó en 1687 la primera gran obra de la Física: Principios matemáticos de filosofía natural, también conocidos como Principia. En la primera de las tres partes en la que se divide la obra, expone en tres leyes las relaciones existentes entre las fuerzas y sus efectos dinámicos: las leyes de la dinámica:
- Primera Ley de Newton o Principio de Inercia.
- Segunda Ley de Newton o Principio Fundamental.
- Tercera Ley de Newton o Principio de Acción Reacción
La segunda ley de Newton o principio fundamental establece que las aceleraciones que experimenta un cuerpo son proporcionales a las fuerzas que recibe. Probablemente su forma más célebre es:
En este apartado vamos a profundizar en su estudio, y veremos que la anterior, aunque muy útil, no es en realidad su forma general. Seguiremos los siguientes puntos:
- Concepto
- Definición
- Generalizaremos mediante la definición diferencial
- Particularizaremos para el caso de que la masa permanezca inalterada
- Definición de newton
Empecemos con fuerza...
Concepto
Imagina dos cuerpos A y B con la misma masa que se mueven a la misma velocidad sobre dos superficies horizontales distintas. Pasado cierto tiempo, A se detiene y un rato más tarde se detiene B. Aunque los dos tienen la misma cantidad de movimiento o momento lineal inicial, A lo pierde antes que B. Por tanto, podemos suponer que la intensidad de la interacción entre los cuerpos y el suelo, que hace que los dos cuerpos terminen deteniéndose, es mayor en el A que en el B.
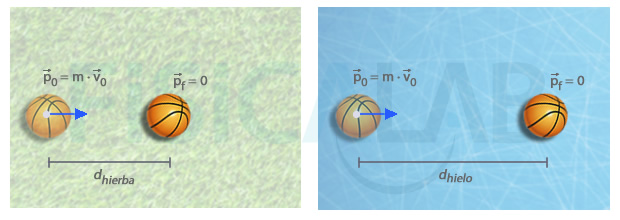
Intensidad interacción en distintas superficies
A la izquierda, lanzamos una bola sobre una superficie rugosa, por ejemplo hierba, con un determinado momento lineal inicial
Así pues, si decimos que la fuerza es la intensidad de la interacción, llegamos a la definición de la segunda ley de Newton.
Definición
La segunda ley de Newton o principio fundamental establece que la rapidez con la que cambia el momento lineal (la intensidad de su cambio) es igual a la resultante de las fuerzas que actúan sobre él:
Donde:
- Δt : Representa el intervalo de tiempo considerado. Su unidad de medida en el S.I. es el segundo
Como puedes ver, este principio relaciona matemáticamente las fuerzas con el efecto que producen, de tal forma que resulta fundamental para resolver cualquier problema de dinámica.
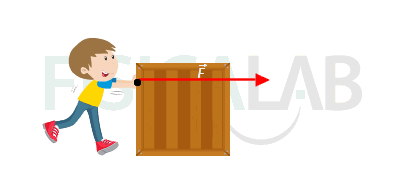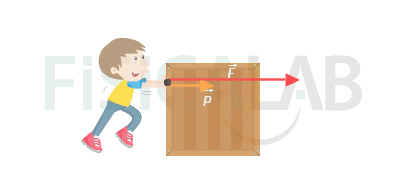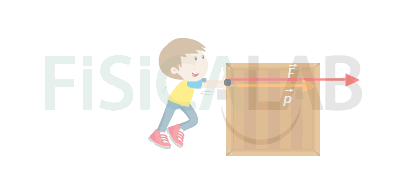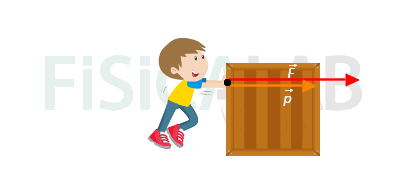
Ejemplo de aplicación de la segunda ley de Newton
Cuando empujas un objeto, por ejemplo una caja, aplicando una fuerza sobre él de manera sostenida, se produce un incremento de su momento lineal, representado por la flecha naranja. Ten presente que siempre que la masa a la que aplicas la fuerza se mantenga constante, el aumento del momento lineal se traducirá en un incremento de su velocidad, pues p=m·v.
Definición diferencial
En la expresión anterior estamos dando por sentado que la fuerza total es constante en el intervalo Δt. En caso de no serlo, la expresión anterior nos proporcionará una fuerza total promedio. Por norma general, las fuerzas no suelen ser iguales durante todo el intervalo de tiempo, por lo que nos resultará de utilidad una ecuación que nos determine la fuerza en un instante concreto de tiempo.
Podemos obtener la fuerza instantánea total calculando la fuerza entre dos instantes de tiempo tan próximos que su intervalo tiende a 0. Es justamente la definición de la derivada y se trata del mismo proceso que seguíamos en el caso de la velocidad instantánea o la aceleración instantánea:
La resultante de las fuerzas que actúan sobre un cuerpo en un instante es proporcional a la variación del momento lineal en ese preciso instante y actúa en la dirección de esta, es decir, en la dirección de la variación de su velocidad.
Ten presente que, estrictamente hablando, la segunda ley de Newton solo es válida en sistemas de referencia inerciales. Para sistemas de referencia no inerciales es necesario incluir las fuerzas ficticias o fuerzas inerciales.
Masa Inalterada
Si un cuerpo durante una interacción no cambia el valor de su masa, se obtiene la famosa ecuación que estudiamos en el nivel anterior: F = m · a. Veámoslo:
A la expresión anterior se la conoce como ecuación fundamental de la dinámica de traslación.
La ecuación fundamental de la dinámica de traslación establece que si la fuerza resultante que se aplica a un cuerpo libre no es nula, este experimentará una aceleración, o lo que es lo mismo, un cambio en su estado de reposo o de movimiento.
Donde:
- m : Es la masa del cuerpo, supuesta constante. Su unidad de medida en el S.I. es el kilogramo (kg)
En ocasiones nos resultará de utilidad descomponer la expresión anterior en las componentes cartesianas ( o en cualquier otro sistema de coordenadas)...
Y a veces también en las componentes intrínsecas...
Por otro lado, Newton llegó a esta conclusión tras realizar una serie de experimentos en los que pudo comprobar que:
- Si se aplica la misma fuerza a cuerpos con distinta masa, se consiguen aceleraciones diferentes.
- La fuerza es directamente proporcional a la aceleración que experimenta el cuerpo, y la constante de proporcionalidad del cuerpo utilizado corresponde con su masa.
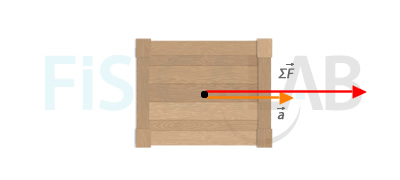
Relación fuerza y aceleración
La fuerza resultante que se aplica en un cuerpo y la consecuente aceleración que aparece en él tienen la misma dirección y sentido. De acuerdo a la segunda ley de Newton, se diferencian en una constante de proporcionalidad: la masa del cuerpo. Así, dado que el vector fuerza resultante de la figura,
Si en la primera ley Newton introdujo el concepto de inercia, en la segunda ley establece cual es su cantidad, es decir, la masa es la magnitud que mide la cantidad de inercia que posee un cuerpo.
Observa que podemos considerar la primera ley de Newton como un caso particular de esta segunda. Efectivamente, cuando...
...es decir, si no hay una fuerza neta actuando sobre un cuerpo, este no varía su cantidad de movimiento, y por tanto, su velocidad permanece constante. Se trata del principio de conservación del momento lineal.
La segunda ley de Newton nos proporciona una relación entre causas, las fuerzas, y los efectos, la aceleración. No dice nada acerca de qué factores influyen en esas causas. Así, por ejemplo, la fuerza de la gravedad depende de las masas y las distancias, la fuerza elástica depende de las características del un muelle y su elongación. Dedicaremos el siguiente tema a estudiar algunas de estas causas y sus aplicaciones.
Definición de newton
La segunda ley de Newton nos permite definir la unidad de fuerza en el Sistema Internacional, el newton.
Se define un newton como la fuerza que hay que aplicar a un cuerpo de 1 kg de masa para comunicarle una aceleración de 1 m/s2. Se abrevia por la letra N. Así:
1 N = 1kg·1m/s2
Y ahora... ¡Ponte a prueba!
Apartados relacionados
Este mismo apartado se encuentra desarrollado en otros niveles educativos. Si sus contenidos no se ajustan al nivel que buscas, prueba a visitar:
