Fuerza Resultante de un Sistema de Fuerzas
Es común que un cuerpo esté siempre sometido a la acción de dos o más fuerzas. En estos casos, el efecto conjunto puede representarse mediante una única fuerza que hace el mismo efecto que todas juntas y que se denomina fuerza resultante. Estudiaremos:
¿Preparado para sumar fuerzas?
Suma de fuerzas concurrentes
Cuando un cuerpo sufre la acción de dos o más fuerzas (sistema de fuerzas), sus efectos pueden ser sustituidos por la acción de una única fuerza denominada fuerza resultante. El proceso mediante el cual se calcula la fuerza resultante recibe el nombre de suma de fuerzas.
La fuerza resultante o fuerza total de un sistema de fuerzas se obtiene mediante la suma vectorial de todas las fuerzas que actúan sobre el cuerpo:
Como sabemos que cada fuerza en el plano OXY, se puede descomponer en función de sus ejes cartesianos
Aclaraciones
A lo largo de este tema consideraremos fuerzas concurrentes, cuyo punto de aplicación siempre será el centro geométrico del cuerpo. Esta consideración da lugar a movimientos de traslación, ya que si no podrían aparecer también movimientos de rotación, como veremos en niveles más avanzados.
Casos particulares
Estudiaremos diferentes casos:
- las fuerzas actúan en la misma dirección y sentido.
- las fuerzas actúan en la misma dirección y sentido contrario.
- las fuerzas actúan en cualquier dirección.
Suma de fuerzas concurrentes con la misma dirección y sentido
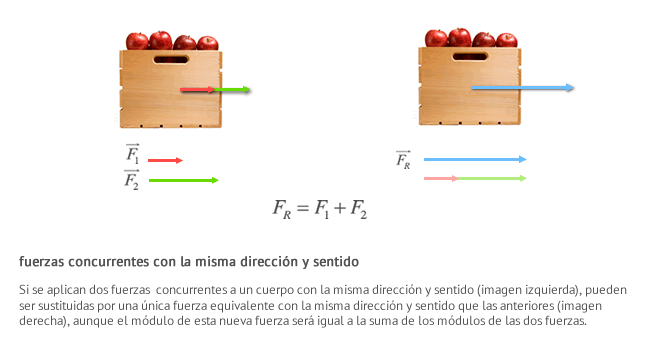
Suma de fuerzas concurrentes con la misma dirección y distinto sentido
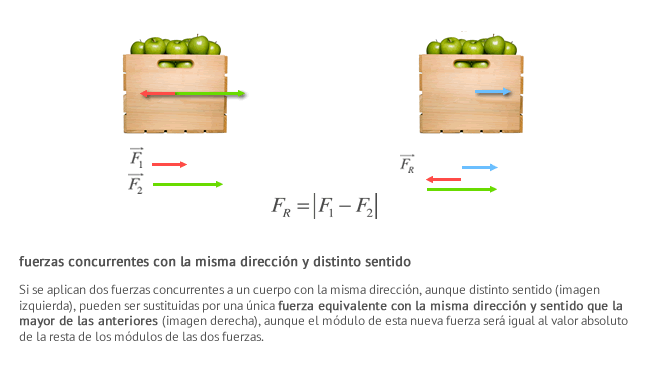
Suma de fuerzas concurrentes con distinta dirección
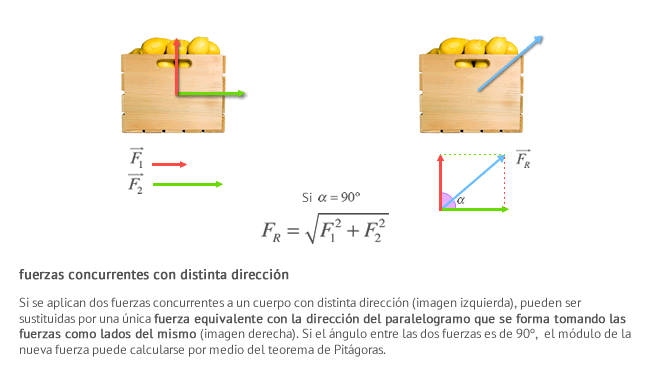
Y ahora... ¡Ponte a prueba!
Apartados relacionados
Este mismo apartado se encuentra desarrollado en otros niveles educativos. Si sus contenidos no se ajustan al nivel que buscas, prueba a visitar:
