Resultant Force of a System of Forces

It is commonly known that a body is always submitted to the action of two or more forces. On these cases, the effect as a whole can be represented throughout a single force that cause the same effect on all the forces and which is called resultant force. We will study:

How to add forces
Some simplifications we can do in particular cases

Ready to add forces?

Concurrent forces addition

When a body is submitted to the action of two or more forces (system of forces), their effects can be replaced by the action of a single force called resultant force. The process through we calculate the resultant force is called addition of forces.

The resultant force or total force of a system of forces is obtained by the vector addition of al the forces acting over the body:

$\sum_{} \vec{F} = \vec{F_{1}} + \vec{F_{2}} + \vec{F_{3}} + . . . + \vec{F_{n}}$

Since we know that every force on the plane OXY can be decomposed depending on its cartesian axes, then:

Clarifications

On this topic we consider concurrent forces, whose application point will always be the geometrical centre of the body. This consideration gives room to translational motion, otherwise, rotational motion could take place as we will see on advanced levels.

Example

If the following forces act on a body: ${\vec{F}}_{1} = - 10 \cdot \vec{i} + 10 \cdot \vec{j} ⋮ {\vec{F}}_{2} = 4 \cdot \vec{i} - 3 \cdot \vec{j} ⋮ {\vec{F}}_{3} = 5 \cdot \vec{i} - \vec{j} ⋮ {\vec{F}}_{4} = \vec{i} - \vec{j}$

Find out a force whose effect is equal to exert the 4 forces proposed.

Solution

Particular cases

We will study different cases:

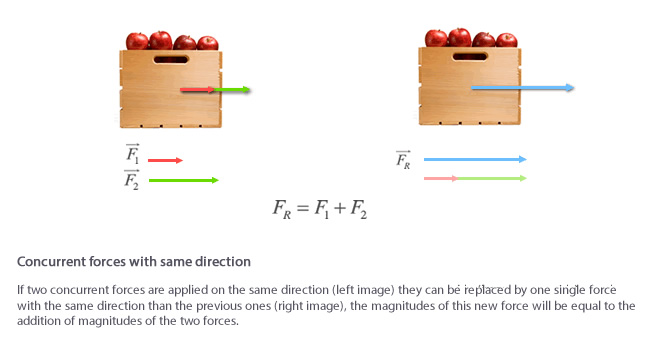
Forces acting on the same direction
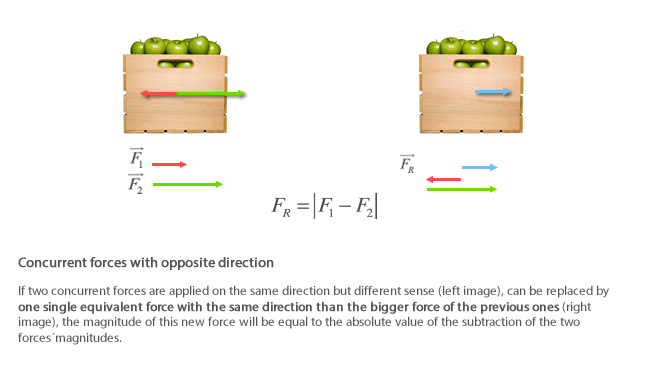
Forces acting on opposite direction
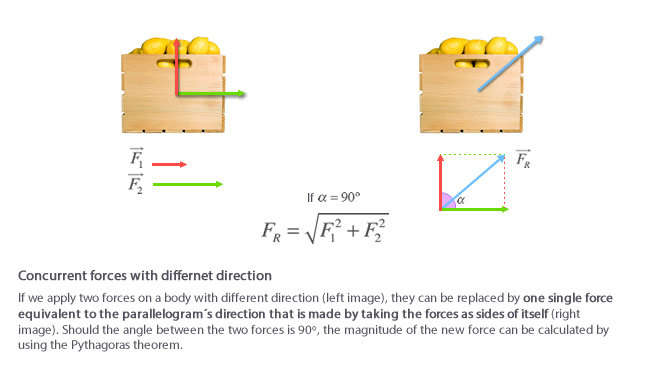
Forces acting on any direction

Addition of concurrent forces on the same direction

adding concurrent forces on same direction

Example

Two friends, a stocky one and a slim one, push a coach on the same direction. The first one exert a force of 11 N and the second one a force of 7 N. What is the resultant force?

Solution

Addition of forces on opposite direction

adding concurrent forces on opposite directions

Example

A boy and a girl tight two cords to a ring and play to find out who is stronger. The boy grab one of the cords and exert a force of 11 N, the girl applies 13 N at the same time. If both pull the cords on different directions... Who will win?

Solution

Addition of forces on any direction

adding concurrent forces on different directions

Experiment & Learn

Data

Addition of concurrent forces

There are two foces in the chart ${\vec{F}}_{1}$ and ${\vec{F}}_{2}$ . Move the red points to modify those forces and observe how we get a force ${\vec{F}}_{R}$ equivalent to the effect both forces produce by the rule of parallelogram.

Check that when they don ́t have the same direction and form an 90º angle, the magnitude ${\vec{F}}_{R}$ is obtained from ${\vec{F}}_{1}$ and ${\vec{F}}_{2}$ throughout the expression:

$F_{R} = \sqrt{{F_{1}}^{2} + {F_{2}}^{2}}$

and if you place them on the same direction (one on top of the other)

$F_{R} = F_{1} + F_{2}$

and with opposite direction (each one looking away)

$F_{R} = |F_{1} - F_{2}|$

Concurrent forces addition

Particular cases

Addition of concurrent forces on the same direction

Addition of forces on opposite direction

Addition of forces on any direction

Now... ¡Test yourself!

Related sections

Site

Contact form

Follow us

Resultant Force of a System of Forces

Ayúdanos a mantenernos en órbita

¿Nuestros contenidos te están resultando de utilidad?

Concurrent forces addition

Particular cases

Addition of concurrent forces on the same direction

Addition of forces on opposite direction

Addition of forces on any direction

Now... ¡Test yourself!

Related sections