Trabajo en el interior de un campo eléctrico
Enunciado
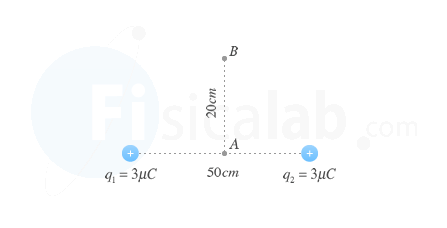
Dado el esquema de la figura, calcula el trabajo eléctrico que realizaría el campo para desplazar una carga q3 = 2 µC desde el punto A hasta el punto B.
Solución
Datos
q1 = 3 µC = 3·10-6 C
q2 = 3 µC = 3·10-6 C
r12 = 50 cm = 0.5 m
rAB= 20 cm = 0.2 m
Consideraciones Previas
Si la distancia entre q1 y q2 es 0.5 m, la distancia entre q1 y A es r1A = 0.25 m y la distancia entre q2 y A es r1A = 0.25 m.
Si la distancia entre A y B es 0.25 m, la distancia entre q1 y B se obtiene aplicando el teorema de Pitágoras, de tal forma que r1B = r1A = 0.32 m.

Resolución
El trabajo eléctrico podemos obtenerlo por medio de la siguiente expresión:
Para ello, es necesario calcular el potencial eléctrico en A (VA) y en B (VB). Lo haremos de forma separada.
VA
El potencial en A es la suma del potencial creado de forma aislada por la carga q1 (V1A) y por la carga q2 (V2A):
VB
De igual forma para B:
Una vez que conocemos los valores de VA y VB podemos calcular el trabajo que realiza el campo eléctrico:
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
