Representación de Vectores

Representación Gráfica

Gráficamente, un vector se representa como una flecha ubicada en un eje de coordenadas. En esta flecha podemos identificar cada uno de los elementos que lo conforman y que estudiamos en el apartado anterior, además de algunos más.

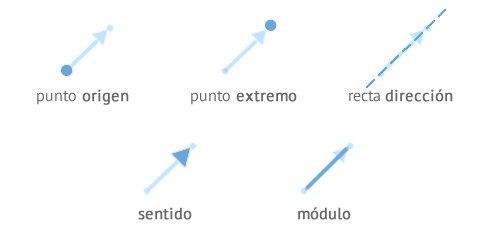
Tienen un punto desde el que nace la flecha llamado origen o punto de aplicación.
De igual forma, tienen otro punto donde termina la flecha llamado extremo.
La recta sobre la que "descansan" los puntos de extremo y origen se denomina dirección o recta soporte.
La distancia entre el punto origen y extremo corresponde con su módulo. A mayor distancia entre ellos, el módulo será mayor.
La punta de la flecha determina su sentido, dentro de los dos posibles que se podría dibujar siguiendo su dirección, es decir hacia un lado de la recta o hacia el otro.

Experimenta y Aprende

Datos

|\vec{a}| = a =

Representación de un vector

Desliza los puntos origen y extremos del vector $\vec{a}$ y comprueba como puedes cambiar su módulo, su dirección y su sentido.

Observa que al acercar los puntos origen y extremo el módulo del vector, que se expresa como $|\vec{a}|$ , disminuye. ¿Qué ocurre si los alejas?.

NOTA. Los puntos discontinuos no se suelen dibujar, los representamos aquí para que puedas ver más clara la dirección del vector.

Representación Analítica

Todo vector se puede expresar como la suma de otros vectores que sirven de patrón o referencia. Estos vectores reciben el nombre de vectores unitarios ya que su módulo vale 1 (módulo unitario). En concreto se emplean:

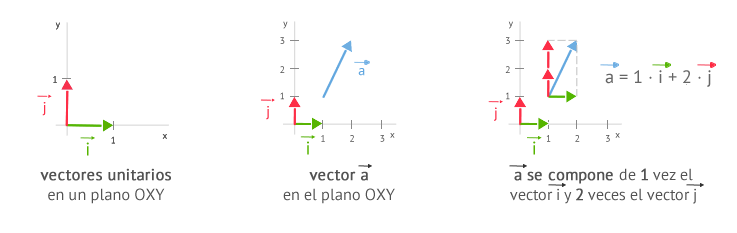
$\vec{i}$ o $\vec{u_{x}}$ es un vector unitario en la dirección del eje X
$\vec{j}$ o $\vec{u_{y}}$ es un vector unitario en la dirección del eje Y

Como se muestra en el ejemplo anterior, hemos obtenido una forma de representar analíticamente un vector a partir de su gráfica. A continuación, puedes encontrar otras formas de representación posibles. De esta forma, un vector $\vec{a}$ con origen en el punto A = (A_x,A_y) y extremo en el punto B = (B_x,B_y) se puede representar analíticamente de la siguientes formas:

	$\vec{a} = a_{x} \cdot \vec{i} + a_{y} \cdot \vec{j}$	donde $a_{x}$ y $a_{y}$ reciben el nombre de componentes cartesianas del vector y se calculan de la siguiente forma: $a_{x} = B_{x} - A_{x}$ $a_{y} = B_{y} - A_{y}$

	$\vec{a} = a_{x} \cdot \vec{u_{x}} + a_{y} \cdot \vec{u_{y}}$
	$\vec{a} = (a_{x}, a_{y})$

Módulo de un Vector

Las coordenadas cartesianas (a_xy a_y) son muy importantes, ya que a partir de ellas es posible calcular el módulo y dirección del vector. Este último, teniendo en cuenta el ángulo $α$ formado entre el vector y el semieje X positivo (o por el ángulo $β$ formado entre el vector y el semieje Y negativo).

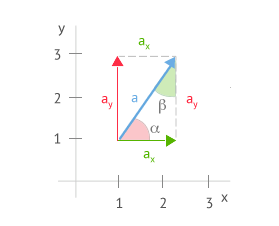
Módulo y coordenadas de un vector

Si aplicamos el teorema de Pitágoras, podemos deducir que

$|\vec{a}| = a = \sqrt{{a_{x}}^{2} + {a_{y}}^{2}}$

Además, si aplicamos las definiciones del seno y del coseno, podemos obtener otra forma de calcular las componentes cartesianas.

$a_{x} = a \cdot \cos (α) = a \cdot \sin (β)$
$a_{y} = a \cdot \sin (α) = a \cdot \cos (β)$

Ejemplo

Dado el siguiente vector:

$\vec{a} = 5 \cdot \vec{i} + 4 \cdot mover$

Represéntalo gráficamente.

Ver solución

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.