Aceleración Instantánea

En Física decimos que un cuerpo tiene aceleración cuando se produce un cambio del vector velocidad, ya sea en módulo o dirección. Así lo hemos visto en el apartado dedicado al concepto de aceleración. En este apartado vamos a estudiar la aceleración instantánea, que representa la variación de velocidad que está teniendo lugar en un instante concreto.

Aceleración Instantánea

La aceleración instantánea de un cuerpo es la que tiene el cuerpo en un instante específico, en un punto determinado de su trayectoria. Para definir el concepto de aceleración instantánea con precisión podemos partir de la aceleración media en un intervalo y hacer este infinitamente pequeño ($∆t\to 0$ ). Este proceso es análogo al que seguíamos con la velocidad media para calcular la velocidad instantánea.

La aceleración es una magnitud vectorial. La ecuación de dimensiones de la aceleración instantánea es [a] = [L][T]^-2 y por tanto su unidad de medida en el Sistema Internacional (S.I.)  es el metro por segundo al cuadrado [m/s²].

Podrás encontrar el vector aceleración escrito mediante sus componentes cartesianas quedando:

• vector aceleración  en 3 dimensiones coordenadas cartesianas:

  $$\overrightarrow{a}=a_x\overrightarrow{i}+a_y\overrightarrow{j}+a_z\overrightarrow{j}=\left(\underset{∆t\to 0}{\lim }\frac{∆v_x}{∆t}\right)\overrightarrow{i}+\left(\underset{∆t\to 0}{\lim }\frac{∆v_y}{∆t}\right)\overrightarrow{j}+\left(\underset{∆t\to 0}{\lim }\frac{∆v_z}{∆t}\right)\overrightarrow{j}=\frac{d{v}_x}{dt}\overrightarrow{i}+\frac{d{v}_y}{dt}\overrightarrow{j}+\frac{d{v}_x}{dt}\overrightarrow{j}$$

• vector aceleración en 2 dimensiones coordenadas cartesianas:

  $$\overrightarrow{a}=a_x\overrightarrow{i}+a_y\overrightarrow{j}=\left(\underset{∆t\to 0}{\lim }\frac{∆v_x}{∆t}\right)\overrightarrow{i}+\left(\underset{∆t\to 0}{\lim }\frac{∆v_y}{∆t}\right)\overrightarrow{j}=\frac{d{v}_x}{dt}\overrightarrow{i}+\frac{d{v}_y}{dt}\overrightarrow{j}$$

Como puedes observar, la aceleración instantánea es una magnitud vectorial que cumple:

• Su módulo se puede expresar:

  • Mediante coordenadas cartesianas en 3 dimensiones:

    $$\left|\overrightarrow{a}\right|=\sqrt{a_x^2+a_y^2+a_z^2}$$

  • Mediante coordenadas cartesianas en 2 dimensiones:

    $$\left|\overrightarrow{a}\right|=\sqrt{a_x^2+a_y^2}$$
• Su dirección y sentido, en general, no coincide con la del vector velocidad sino que dependen del cambio que experimente esta.

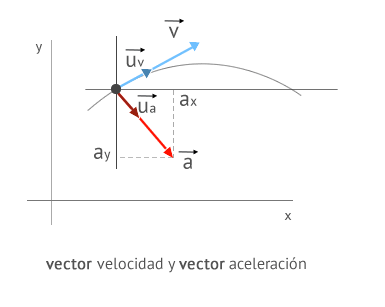
No confundas las componentes cartesianas de la aceleración con las componentes intrínsecas, que estudiaremos en apartados posteriores. Las componentes cartesianas son, simplemente, la descomposición del vector aceleración en los ejes cartesianos. Las componentes intrínsecas son la descomposición del vector aceleración en el sistema de referencia propio o intrínseco del movimiento, como estudiarás en el apartado dedicado a ello.

Por último indicarte que, al igual que cualquier otro vector, es posible que en ocasiones encuentres el vector aceleración escrito en función de su módulo. Para ello basta multiplicar el módulo del vector aceleración por un vector unitario con la misma dirección y sentido que $\overrightarrow{a}$  y que llamaremos ${\overrightarrow{u}}_a$  por ser el vector unitario que contiene la dirección del vector aceleración.

$$\overrightarrow{a}=a\cdot {\overrightarrow{u}}_a$$