Angular quantities, also known as angular magnitudes, as its name suggests, are related to angles. Among other things they allow us to study circular motion. In this section, we are going to present you the main ones. We will see:
- Units for measuring angles: radians and degrees
- Angular position
- Displacement in relation to an angle: angular displacement
- What the angular velocity is
- The expression for angular acceleration
- A review of normal acceleration
- The relationship between angular and linear quantities
- A brief introduction to angular quantities as vectors
Radians and Degrees
The International System (S.I.) unit for measuring angles is the radian (rad). A circumference is 2π radian. Contrariwise, we can also measure angles in degrees. A circle has 360 degrees. Considering the previous relationship, to convert degrees to radians, you can use the following expression:
Angular Position
The angular position φ is a fundamental angular magnitude which represents the angle that the position vector of a body forms with the positive side of the x-axis or positive x-semiaxis. Its unit in the International System (SI) is the radian (rad).
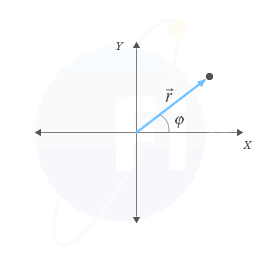
Angular position φ
The angular position corresponds to the angle that the position vector of a body form with the positive side of the x-axis or positive x-semiaxis
Angular Displacement
The angular displacement (Δφ) represents the traveled angle. It is given by the difference between φf , the final angular position, and the initial angular position φi:
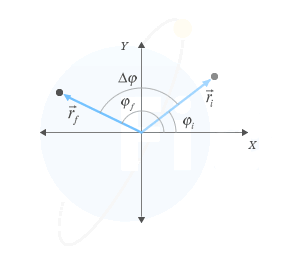
Angular displacement Δφ
The angular displacement corresponds to the angle traveled by a body moving from an initial angular position φi to a different final one φf
Angular Velocity
It represents the angular displacement (Δφ) experienced by a body each second. Its unit in the International System (SI) is the rad/sec although sometimes you will see that you can also use revolutions per minutes, rpm (1 r.p.m. = 2π/60 rad/s). As it happened with velocity, there is an average angular velocity ωa and an instantaneous angular velocity ω (or simply angular velocity) according to the time considered, whether a time interval Δt or an instant of time dt, respectively.
| ωa | ω |
|---|---|
Angular Acceleration
It represents the variation of the angular velocity (Δω) with time. Its unit in the International System (SI) is the rad/s2. Just like with equivalent linear quantities, there is an average angular acceleration αa and an instantaneous angular acceleration α (or simply angular acceleration) according to whether an interval of time ∆t or an instant of time respectively dt is being considered.
| αa | α |
|---|---|
Normal or Centripetal Acceleration
Although it is not an angular magnitude properly speaking, because it is not measured in angular units, it is important to remember here the expression for normal or centripetal acceleration.
Remember that normal or centripetal acceleration is responsible for the change of direction of the velocity vector so it appears in all circular motions.
Relationship between Angular and Linear Quantities
We can relate angular and linear quantities in circular motions using the radius R.
| Linear quantity | Relationship | Angular quantity |
|---|---|---|
| s | φ | |
| v | ω | |
| at | α | |
| an | - |
Angular Vectors Quantities
So far we have studied the angular quantities as scalars. In reality, they are vector magnitudes, but for the purposes of this level, we will consider them scalars. However, here we anticipate the relationship of linear velocity with angular velocity and tangential acceleration with angular acceleration, in vector form, which is given by the vector product:

