Ecuación de onda a partir de gráficas

Datos

Nos proporcionan dos gráficas.

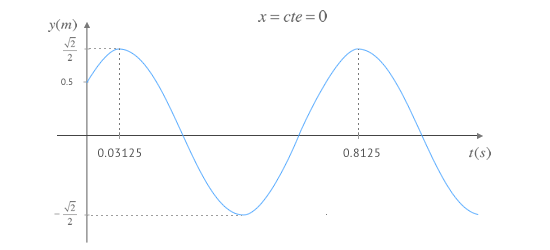
• La primera de ellas representa la elongación y de una partícula, situada en x=0, en función del tiempo t. Es decir, nos permite apreciar la evolución temporal de la onda. Cualquier partícula alcanzada por la onda seguirá un movimiento similar, esto es, su función será también un seno pero con cierto desfase respecto al de x=0 representado
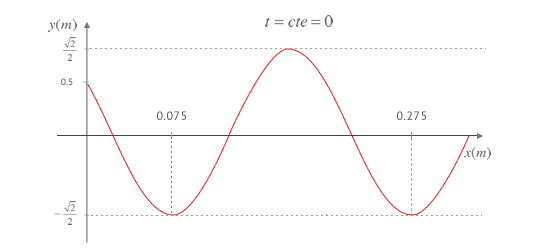
• La segunda de ellas representa la elongación de las partículas situadas a distancia x del origen en un instante t=0. Nos permite apreciar la evolución espacial de la onda

Resolución

Se trata claramente de una onda armónica, por tener las gráficas formas sinusoidales, que se propaga en el sentido positivo del eje x. Sabemos que la ecuación de una onda armónica que se propaga hacia la derecha viene dada, en una de sus múltiples formas equivalentes, por: 

$$y=A·\sin \left(\omega ·t-k·x+{\phi }_0\right)$$ 

De cualquiera de las dos gráficas podemos obtener la amplitud A. $A=\frac{\sqrt{2}}{2}$ . Por otro lado, de la primera de las gráficas ( x=cte=0 ) podemos obtener el periodo, es decir, cada cuando se repite la onda. T=0.28125-0.03125=0.25 s. La segunda de las gráficas ( t=cte=0 ) nos permite obtener la longitud de onda, como la distancia mínima a partir de la cual la onda comienza a repetirse: λ=0.275-0.075=0.2 m. Las siguientes gráficas recogen lo anterior:

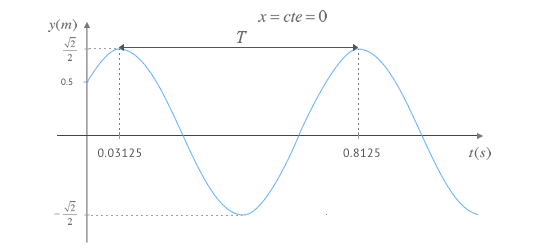
A partir del periodo T podemos obtener ω según:

$$T=\frac{1}{f}=\frac{1}{{\displaystyle \frac{\omega }{2·\pi }}}=\frac{2·\pi }{\omega }\Rightarrow \omega =2·\pi /T=2·\pi /0.25=8·\pi rad/s$$

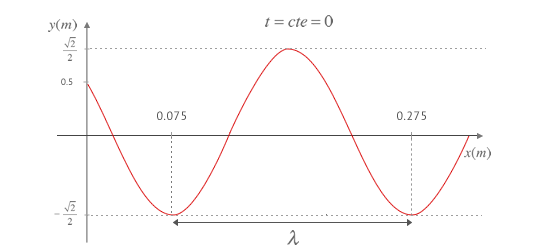
Y a partir de la longitud de onda λ podemos obtener el número de onda k según:

$$k=\frac{2·\pi }{\lambda }=\frac{2·\pi }{0.2}=10\pi rad/m$$

Finalmente, de cualquiera de las dos gráficas podemos obtener también φ₀. Necesitaremos un par de valores. Sabemos que para x=0 y t=0, y=0.5 m, es decir:

$${\overline{)y}}_{x=0,t=0}=0.5=\frac{\sqrt{2}}{2}\sin \left(\omega ·0.5-k·0+{\phi }_0\right)\Rightarrow \frac{1}{\sqrt{2}}=\sin \left({\phi }_0\right)\Rightarrow {\phi }_0=\left\{\begin{array}{l}\frac{\pi }{4}\\ \frac{3·\pi }{4}\end{array}\right.$$

Ahora bien, ¿cuál es el valor correcto para φ₀ de los dos posibles? Utilizaremos un nuevo valor de las gráfica:

$${\overline{)y}}_{x=0,t=0.03125}=\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{2}·\sin \left(8·\pi ·0.03125+{\phi }_0\right)\Rightarrow 1=\sin \left(0.25·\pi +{\phi }_0\right)\Rightarrow {\phi }_0=\left\{\begin{array}{l}\frac{\pi }{4}\\ \cancel{\frac{5·\pi }{4}}\end{array}\right.$$ 

Ya estamos en condiciones de determina la ecuación de onda armónica pedida:

$$\boxed{y\left(x,t\right)=\frac{\sqrt{2}}{2}·\sin \left(8·\pi ·t-10·\pi ·x+\frac{\pi }{4}\right) m}$$