Ondas estacionarias en tubos de aire
Enunciado
Las variaciones de presión que se producen en el aire que hay en el interior de un tubo hueco puede dar lugar a ondas estacionarias, tal y como se pone de manifiesto en la mayoría de los instrumentos de viento. Estas ondas no son más que otro ejemplo de ondas mecánicas en las que el desplazamiento longitudinal de las ondas hace que la presión del aire varíe armónicamente.
Imagina un tubo abierto por uno de sus extremos por donde soplamos o entra aire. En el extremo abierto las moléculas tienen total libertad de movimiento: es lo que se llama un vientre de desplazamiento. En el extremo cerrado, donde se debe reflejar la onda, habrá, por el contrario, un nodo de desplazamiento: las moléculas no tienen posibilidad de moverse. (Observa en este punto que los nodos de desplazamiento corresponden con vientres de presión y viceversa).
Determina qué longitudes de onda y frecuencias que serán capaces de generar una onda estacionaria teniendo en cuenta que la longitud del tubo es L y que la velocidad del sonido en el aire es, aproximadamente, de 340 m/s. ¿Qué ocurriría si el tubo estuviese abierto por ambos extremos?
Solución
Datos
- Longitud del tubo: L
- Velocidad del sonido en el aire: v=340m/s
Consideraciones previas
La ecuación de las ondas estacionarias en los tubos es similar a la de las ondas estacionarias en cualquier otro medio, es decir en la forma de
Resolución
Como nos dice el enunciado, en un tubo abierto sólo por uno de sus extremos habrá un nodo de desplazamiento en el extremo cerrado y un vientre en el abierto, de manera que podemos encontrar la siguiente relación entre la longitud de onda y la longitud del tubo según:
Donde n=1,3,5…, es decir, sólo existen los armónicos impares. Por otro lado, podemos relacionar las longitudes de onda con las frecuencias de los armónicos a partir de la velocidad de la onda:
Donde el valor de v será de 340 m/s. La imagen siguiente te puede servir de ayuda para visualizar las expresiones anteriores:
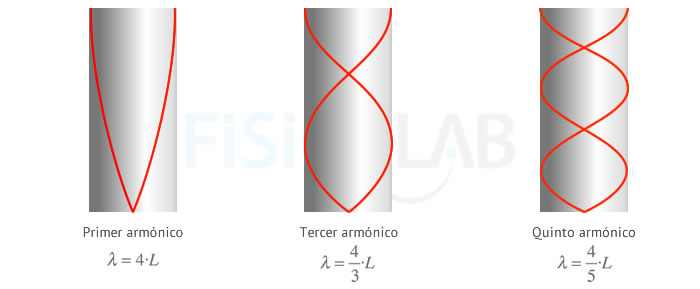
En caso de que ambos extremos estén abiertos, lo que tenemos es dos vientres de desplazamiento. Sabemos que los vientres se encuentran separados al menos λ/2, por lo que:
Donde n=1,2,3…, es decir, existen todos los armónicos en este caso. Una vez más, podemos relacionar las longitudes obtenidas con las frecuencias posibles de los armónicos a partir de la velocidad de la onda quedando:
Donde el valor de v será de 340 m/s. La imagen siguiente te puede servir de ayuda para visualizar las expresiones anteriores:
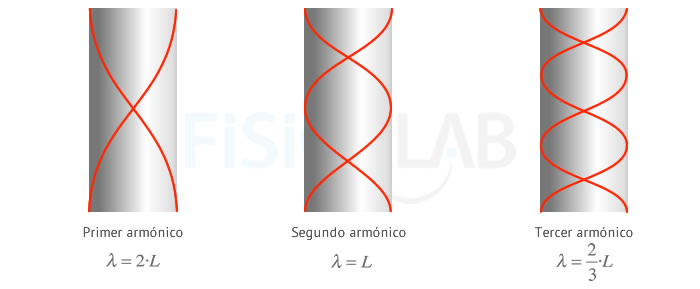
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
