Gráfica, desplazamiento y velocidad de onda estacionaria
Enunciado
Una onda estacionaria se encuentra descrita por la siguiente función
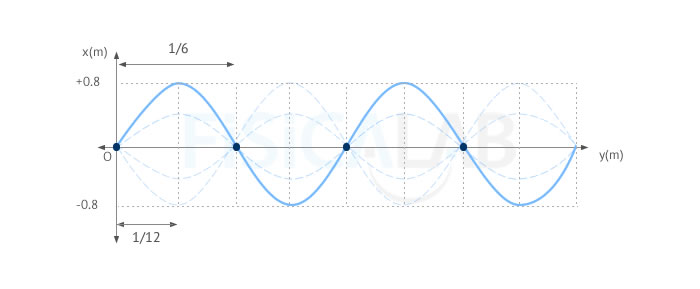
- Realiza una gráfica de la onda estacionaria.
- ¿Cuál es el máximo desplazamiento que experimenta un punto que se encuentra a 5/12 m del origen?¿Y uno que se encuentre a 0.35 m?
- ¿Cual es la máxima velocidad que alcanza un punto que se encuentra a 5/12 m del origen?¿Y uno que se encuentre a 0.35 m?
Solución
Datos
- La ecuación de la onda estacionaria
- Distancia del punto 1 al origen x1 = 5/12 m
- Distancia del punto 2 al origen x2 = 0.35 m
Resolución
Sabemos que la onda estacionaria oscila entre su máximo (0.8) y su mínimo (-0.8). Buscaremos la posición de los vientres y los nodos a fin de poder representarla.
Vientres:
Nodos:
La longitud de onda es
Para determinar el máximo desplazamiento dmax de un punto a una determinada distancia del origen xi calculamos su amplitud resultante (AT). La elongación de dicho punto variará entre -AT y AT, dependiendo del signo de cos(ω·t) (dicha partícula no describe más que un m.a.s cuya amplitud está dada por AT). Por tanto, el máximo desplazamiento será dmax=2·AT. Recuerda que AT es el término que acompaña a cos(ω·t) en la ecuación de la onda estacionaria, es decir: AT=0.8·sin(6·π·x). En realidad, para un valor xi concreto AT puede ser positivo o negativo (según el signo de sin(6·π·xi)). Pero sólo nos interesará el valor positivo (valor absoluto) para determinar el desplazamiento, siendo más correcto escribir dmax=2·|AT|.
Considerando el primer punto x1=5/12 nos queda que el máximo desplazamiento dmax:
Observa que dicho punto corresponde a un vientre (5/12 = (2·n+1)/12 con n = 2).
Considerando el segundo punto x2=0.35, nos queda que el máximo desplazamiento dmax:
Por lo que no se trata de un vientre ni de un nodo.
En relación a la velocidad máxima, esta se producirá cuando las partículas pasen por la posición de equilibrio, es decir, y=0. En cualquier caso, y dado que la ecuación de la onda estacionaria nos marca la posición y, derivando dicha posición respecto al tiempo obtenemos la ecuación de la velocidad, tal y como vimos al estudiar la velocidad del m.a.s.
Si consideramos el primer punto x1=5/12, y teniendo en cuenta que el valor máximo de velocidad se producirá cuando sin(15·π·t) valga 1 o -1, nos queda:
Mientras que en el caso de x2=0.35, tenemos:
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
