Energía potencial elástica y gravitatoria en muelle

Enunciado

dificultad

Sobre una plataforma situada sobre un muelle vertical de K = 9 N/cm se sitúa una caja de 0.5 kg. Una vez que se alcanza el equilibrio mecánico, calcula el trabajo necesario para bajar dos centímetros más la caja.

Solución

Datos

Constante elástica del muelle K = 9 N/cm = 900 N/m
Masa del cuerpo: 0.5 kg
∆y_extra= 2 cm = 2·10^-2 m

Consideraciones previas

Se hace necesario conocer la distancia inicial al punto de equilibrio. Cuando se sitúa la caja sobre el muelle, este se comprime. Se alcanza el equilibrio cuando el módulo del peso igual al módulo de la fuerza elástica. Esta última sigue la Ley de Hooke
En la caja existen dos tipos de energía potencial, la elástica y la gravitatoria. Aunque no podemos conocer la energía potencial gravitatoria de cada punto, pues no sabemos a que altura sobre el suelo se encuentra la caja, si que podemos conocer la diferencia de energía potencial entre dos puntos.
Para mover 2 cm más la caja, calculamos la diferencia de energía potencial total (elástica más gravitatoria) en el punto inicial y en el punto final. El trabajo necesario para mover la caja esos 2 cm extras lo realiza una fuerza externa y coincide con la diferencia de energía potencial total entre ambos puntos
Consideramos el valor de g = 9.8 m/s
La siguiente imagen representa la situación:

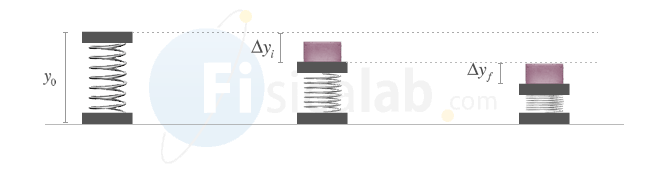
Resolución

Comenzamos calculando la distancia inicial del muelle al punto de equilibrio ∆y_i, una vez alcanzado el equilibrio mecánico, es decir, cuando se igualan el peso y la fuerza elástica inicial en módulo.

$P = F_{e_{i}} \Rightarrow m \cdot g = k ∆ x_{i} \Rightarrow ∆ x_{i} = \frac{m \cdot g}{K} = 5.45 \cdot 10^{- 3} m$

Calculamos ahora la diferencia de energía potencial gravitatoria de la caja entre la posición inicial y final:

$∆ E_{p_{g}} = m \cdot g \cdot ∆ h = 0.5 \cdot 9.8 \cdot (- 2 \cdot 10^{- 2}) = - 0.098 J$

Calculamos la diferencia de energía potencial elástica entra la posición inicial y final

$∆ E_{p_{e}} = E_{p_{e_{f}}} - E_{p_{e_{i}}} = \frac{1}{2} \cdot k \cdot (∆ x_{i} + ∆ x_{f})^{2} - \frac{1}{2} \cdot k \cdot ∆ {x_{i}}^{2};$

$∆ E_{p_{e}} = \frac{1}{2} \cdot 900 \cdot (5.45 \cdot 10^{- 3} + 2 \cdot 10^{- 2})^{2} - \frac{1}{2} \cdot 900 \cdot (2 \cdot 10^{- 2})^{2} = 0.111 J$

Calculamos la diferencia de energía potencial como la suma de las diferencias de la energía potencial elástica y la gravitatoria:

$∆ E_{p} = ∆ E_{p_{g}} + ∆ E_{p_{e}} = - 0.098 + 0.111 = 0.013 J$

Para variar la energía potencial debe invertirse un trabajo externo que coincide en valor exactamente con esa variación de energía potencial (fuerzas conservativas):

$W = ∆ E_{p} = 0.013 J$

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Fórmulas

Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.

Fórmulas

Apartados relacionados