Campo Gravitatorio en la Tierra

La Tierra cuenta con una masa aproximada de 5.974·10²⁴ kg. Este enorme valor hace que los efectos del campo gravitatorio que genera sean muy evidentes: no tienes más que dar un salto para darte cuenta de que la Tierra te atrae con una gran intensidad. En este apartado vamos a tratar, precisamente, del campo gravitatorio generado por la Tierra y algunas particularidades que presenta. Veremos:

• La intensidad de campo en la superficie terrestre
• Su variación con la altitud y como se asocia a la ingravidez
• Su variación con la latitud y como se asocia a la gravedad efectiva y al peso aparente
• Como deducir el valor de energía potencial en las proximidades de la superficie terrestre

¿Listo?

Intensidad de campo en la superficie

Comprobación

Para determinar la intensidad del campo gravitatorio creado por la Tierra en un punto cualquiera de su superficie consideraremos:

• La Tierra como una esfera sólida formada por un conjunto de campas concéntricas uniformes. No olvides, no obstante, que en realidad la Tierra está un poco achatada por los polos
• Que el radio medio de la Tierra R_T es de 6371 km
• Que su masa M_T es de, aproximadamente 5.974·10²⁴ kg

Se trata de aproximaciones que nos permitirán hacer cálculos que arrojarán valores cercanos muy cercanos a los reales.

Recordamos que la intensidad de campo en el exterior de una esfera viene dada por la expresión:

$$\overrightarrow{g}=-G·\frac{m}{r^2}·{\overrightarrow{u}}_r$$

Donde G  es la constante de gravitación universal, m  es la masa del cuerpo que genera el campo, r  es el módulo del vector $\overrightarrow{r}$  que une el centro de la masa con el punto en el cual queremos determinar el campo y ${\overrightarrow{u}}_r$  es el vector unitario de $\overrightarrow{r}$ 

Por tanto, para determinar el valor de la intensidad de campo en la superficie de la Tierra sustituimos por los valores señalados.

$$\begin{gathered} {\overrightarrow{g}}_0=-G·\frac{M_T}{{R_T}^2}·{\overrightarrow{u}}_r=-6.67·{10}^{-11}·\frac{5.974·{10}^{24}}{{\left(6371·{10}^3\right)}^2}·{\overrightarrow{u}}_r=-9.8·{\overrightarrow{u}}_r N/kg\Rightarrow \\ \Rightarrow g_0=9.8 N/kg=9.8 m/s^2 \end{gathered}$$

Como no puede ser de otra manera, la dirección y sentido del campo siempre es normal a la Tierra y apuntando hacia su centro, tal y como se derivan de la multiplicación por el vector unitario ${\overrightarrow{u}}_r$  y del signo -.

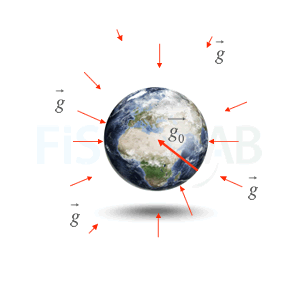
Intensidad del campo gravitatorio en la superficie de la Tierra

El vector intensidad de campo gravitatorio $\overrightarrow{g_0}$ en la superficie terrestre es perpendicular a la misma y apuntando hacia su centro.

El valor obtenido es un promedio que varía localmente en función de la altura, de la latitud y de la composición del subsuelo.

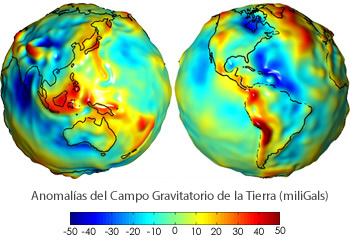
Anomalías en la superficie terrestre

Las variaciones en la composición del subsuelo como pueden ser, por ejemplo, la yacimientos minerales o petrolíferos, causan anomalías locales que afectan al valor de $\overrightarrow{g_0}$. Para medir dichas anomalías suelen usarse mapas de anomalías como el de la figura. La unidad de medida de dichas anomalias suele ser el miligal (1 mGal = 10^-5 N/kg).

Variación con la altitud e ingravidez

Comprobación

La expresión de la intensidad de campo es inversamente proporcional a la distancia r al centro de la esfera considerada, la Tierra en este caso. De esta manera, para un punto que se encuentre a una altura h sobre la superficie, podemos escribir que dicho punto se encuentra a una distancia $r=R_T+h$  del centro de la Tierra, quedando la intensidad del campo en la forma:

$$\overrightarrow{g}=-G·\frac{m}{r^2}·{\overrightarrow{u}}_r=-G·\frac{M_T}{{\left(R_T+h\right)}^2}·{\overrightarrow{u}}_r$$

La expresión anterior puede ser escrita en función del campo en la superficie ${\overrightarrow{g}}_0=-G·\frac{M_T}{{R_T}^2}·{\overrightarrow{u}}_r$  en la forma:

$$\boxed{\overrightarrow{g}={\overrightarrow{g}}_0·\frac{{R_T}^2}{{\left(R_T+h\right)}^2}}$$

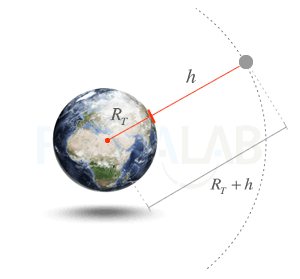
Distancia al centro de la Tierra

Para determinar determinar la distancia r al centro de la Tierra sumamos al valor del radio terrestre R_T la altura h sobre la superficie.

r = R_T + h

Por tanto, a medida que aumenta la altura h sobre la superficie, disminuye la intensidad de campo, haciéndose cero en el infinito. Esto contradice, por ejemplo, la supuesta ingravidez que experimentan los astronautas en el espacio a alturas que distan mucho de ser infinitas. En realidad, dicha ingravidez es fruto de una "caída libre circular" continua que experimentan astronautas y naves, provocando una pérdida de peso aparente.  similar a la que puedes experimentar por ejemplo cuando comienza el descenso de un ascensor.

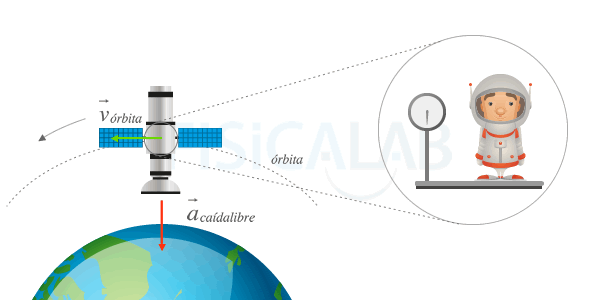
Ingravidez de los astronautas que orbitan alrededor de la Tierra

El efecto de ingravidez experimentado por los astronautas y naves que orbitan la Tierra se debe fundamentalmente a la pérdida de peso aparente que es fruto de la caída libre contínua que tiene lugar.

Variación con la latitud: gravedad efectiva y peso aparente

Comprobación

La Tierra es un cuerpo en permanente estado de rotación sobre sí, lo que hace que cualquier otro cuerpo situado sobre la superficie de la misma (salvo si se sitúa en su eje de rotación) describa un movimiento circular de radio r. Desde un punto de vista intrínseco, es decir, del propio objeto sobre la Tierra, este constituye un sistema de referencia no inercial y, como tal, sobre el cuerpo aparecerá una fuerza centrífuga que hará que el valor efectivo de la gravedad ${\overrightarrow{g}}_{efectiva}$ que actúa sobre el cuerpo varíe ligeramente respecto al que habría si el planeta estuviese en reposo. La siguiente imagen ilustra las aceleraciones a la que está sometido un cuerpo situado en un punto A sobre la superficie terrestre en una latitud determinada por α:

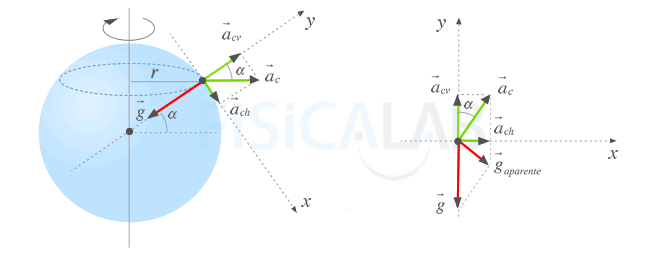
Gravedad aparente

A la izquierda, la Tierra. Es un cuerpo en rotación y cualquier otro cuerpo sobre su superficie situado a una determinada latitud α experimenta la aceleración propia de la gravedad $\overrightarrow{g}$ así como una aceleración centrífuga $\overrightarrow{a_c}$. Dicha aceleración centrífuga puede descomponerse en una componente horizontal $\overrightarrow{a_{ch}}$ y otra vertical $\overrightarrow{a_{cv}}$.

A la derecha la gravedad efectiva, fruto de la suma vectorial de la gravedad $\overrightarrow{g}$ con la aceleración centrífuga $\overrightarrow{a_c}$.

A partir de la imagen podemos encontrar las siguientes relaciones:

$$\begin{gathered} r=R_T·\cos \left(\alpha \right); \\ {\overrightarrow{a}}_c={a_c}_h·{\overrightarrow{u}}_h+{a_c}_v·{\overrightarrow{u}}_v; \\ {a_c}_h=a_c·\sin \left(\alpha \right); \\ {a_c}_v=a_c·\cos \left(\alpha \right); \end{gathered}$$ 

Donde hemos considerado ${\overrightarrow{u}}_h$  y ${\overrightarrow{u}}_v$  los vectores unitarios que definen las direcciones de los ejes intrínsecos horizontal y vertical respectivamente. Ahora bien, recordemos que desde un punto de vista intrínseco, y para el caso del movimiento circular, el valor o módulo de la aceleración centrífuga y el de la normal o centrípeta deben coincidir, quedando:

$$a_c={\omega }^2·r$$

Con lo que podemos escribir:

$$a_c={\omega }^2·R_T·\cos \left(\alpha \right)\Rightarrow \left\{\begin{array}{l}{a_c}_h={\omega }^2·R_T·\cos \left(\alpha \right)·\sin \left(\alpha \right)\\ a_{c_v}={\omega }^2·R_T·{\cos }^2\left(\alpha \right)\end{array}\right.$$

Ya que ${\overrightarrow{g}}_{efectiva}=\overrightarrow{g}+{\overrightarrow{a}}_c$ , si realizamos la suma vectorial obtenemos:

$$\begin{gathered} {\overrightarrow{g}}_{efectiva}=-g·{\overrightarrow{u}}_v+{\omega }^2·R_T·\cos \left(\alpha \right)·\sin \left(\alpha \right)·{\overrightarrow{u}}_h+{\omega }^2·R_T·{\cos }^2\left(\alpha \right)·{\overrightarrow{u}}_v\Rightarrow \\ \Rightarrow \boxed{{\overrightarrow{g}}_{efectiva}=\left({\omega }^2·R_T·\cos \left(\alpha \right)·\sin \left(\alpha \right)\right)·{\overrightarrow{u}}_h+\left({\omega }^2·R_T·{\cos }^2\left(\alpha \right)-g\right)·{\overrightarrow{u}}_v} \end{gathered}$$

En ocasiones se suele despreciar la componente horizontal quedando simplemente ${\overrightarrow{g}}_{efectiva}=-\left(g-{\omega }^2·R_T·{\cos }^2\left(\alpha \right)\right)·{\overrightarrow{u}}_v$ .

Por otro lado, resulta directo calcular el peso efectivo o aparente asociado a la gravedad efectiva como:

$$\boxed{{\overrightarrow{P}}_{aparente}={\overrightarrow{P}}_{efectivo}=m·{\overrightarrow{g}}_{efectiva}}$$

Energía potencial en las proximidades del suelo

La energía potencial de un cuerpo de masa m sobre la superficie de la Tierra, de masa M y radio R_T viene dada por:

$$E_p=-G·\frac{M·m}{R_T}$$

Si situamos el cuerpo a cierta altura h sobre la superficie ( r = R_T + h ), la energía potencial gravitatoria es:

$$E_p=-G·\frac{M·m}{R_T+h}$$

La variación de energía potencial entre ambos puntos:

$$∆E_p=-G·\frac{M·m}{R_T+h}-\left(-G·\frac{M·m}{R_T}\right)=G·M·m\left(\frac{h}{{R_T}^2+R_T·h}\right)$$

Ahora bien, sabemos que R_T >> h, por lo que podemos despreciar R_T·h frente a R_T². También sabemos que, en la superficie terrestre, g₀ = G·M/R_T². Con esto podemos escribir:

$$∆E_p=E_{p_h}-E_{p_{sup}}=m·g_0·h$$ 

Finalmente, si consideramos la energía potencial sobre la superficie 0, $E_{p_{sup}}=0$ , obtenemos el valor de la energía potencial gravitatoria en las proximidades del suelo, tan usado en niveles anteriores:

$$\boxed{E_p=m·g_0·h}$$