Cargas en un triángulo equilatero
Enunciado
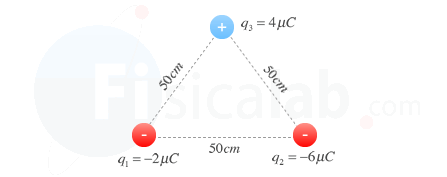
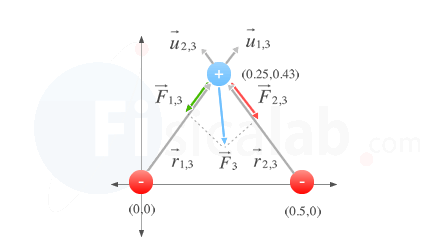
Dado el sistema de cargas de la figura, determina el valor de la fuerza que experimenta q3 sabiendo que las tres cargas se encuentran en el vacío.
Solución
Datos
K = 9·109 N·m2/C2
r13 = r12 = r23 = 50 cm = 0.5 m
q1 = -2 µC = -2·10-6 C
q2 = -6 µC = -6·10-6 C
q3 = 4 µC = 4·10-6 C
Resolución
Antes de comenzar a resolver el ejercicio, lo ideal es elegir un sistema de referencia y situar dichas cargas dentro del sistema. Por simplicidad, posionaremos el origen de coordenadas encima de q1.
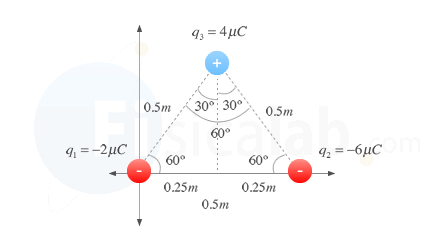
Si observamos la figura nos daremos cuenta de que la posición de q1 y q2 es:
- q1 (0,0) m
- q2 (0.5,0) m
Sin embargo, calcular la posición de q3 no es algo tan trivial. La componente x será la mitad de la distancia entre q1 y q2 (x = 0.25 m) y para calcular la componente y tendremos que hacer uso de la definición de coseno (o alternativamente del teorema de Pitágoras) teniendo en cuenta que en un triángulo equilatero todos sus ángulos poseen 60º y que cada triángulo equilatero se puede descomponer en dos triángulos rectángulos. Girando uno de ellos obtenemos:
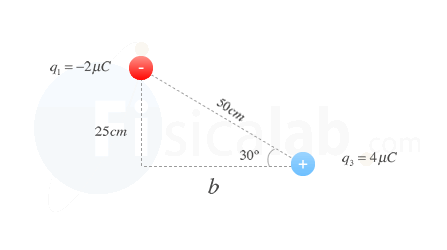
De esta forma para calcular la altura (b) a la que se encuentra la carga q3, basta con aplicar la definición de coseno:
Por tanto la posición de nuestras cargas es:
- q1 (0,0) m
- q2 (0.5,0) m
- q3 (0.25,0.43) m
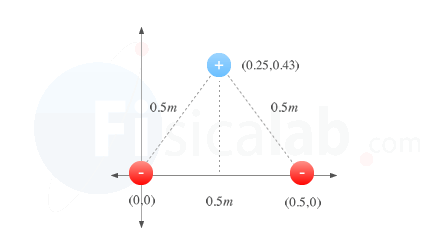
Aplicando el principio de superposición de fuerzas eléctricas, la fuerza (
- la fuerza que ejerce q1 sobre q3 (
- la fuerza que ejerce q2 sobre q3 (
Estudiando cada fuerza por separado tenemos que:
Fuerza
De todos los valores que necesitamos para calcular
Como conocemos la posición de q1 y q3, conocemos los puntos extremo y origen del vector
De aquí sabemos que:
Por tanto:
Fuerza
Aplicando los mismos pasos que para la fuerza anterior:
Una vez que hemos calculado ambas fuerzas, ya estamos en disposición de calcular la fuerza resultante que ejercen q1 y q2 sobre q3:
Por ultimo, para obtener su valor numérico calcularemos su módulo:
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
