Producto de un Número por un Vector

En este apartado vamos a estudiar el producto de un número por un vector a través de los siguientes puntos:

Representación gráfica
Representación analítica
Vector nulo y vector opuesto
División de un vector entre un número

Para que puedas entender con facilidad los conceptos que aquí te presentamos debes conocer qué son los vectores. ¡Vamos a ello!

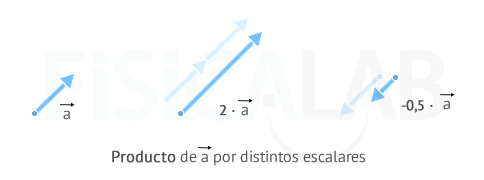
Representación gráfica

Al multiplicar un vector $\vec{a}$ por un escalar (número) $λ$ , obtenemos un nuevo vector $\vec{b} = λ \cdot \vec{a}$ que tiene las siguientes características:

La dirección de $\vec{a}$ y $\vec{b}$ son la misma
Si λ es:
- positivo. $\vec{a}$ y $\vec{b}$ tendrán el mismo sentido
- negativo. $\vec{a}$ y $\vec{b}$ tendrán sentido contrario
El módulo de $\vec{b}$ será el valor absoluto de sumar λ veces el módulo de $\vec{a}$ o lo que es lo mismo $|\vec{b}| = |λ| \cdot |\vec{a}|$ . Los vectores $\vec{a}$ y $\vec{b}$ son por tanto vectores proporcionales que cumplen:
- Si |λ|>1 $\vec{b}$ crece respecto a $\vec{a}$
- Si |λ|<1 $\vec{b}$ decrece respecto a $\vec{a}$
- Si |λ|=1 el vector original no cambia de tamaño

De esto se desprende una ecuación muy interesante. Y es que:

Cualquier vector $\vec{a}$ puede expresarse como un producto de un escalar y otro vector. El producto entre su módulo $|\vec{a}|$ y el vector unitario (vector de módulo 1) ${\vec{u}}_{a}$ que coincide con la dirección y sentido de dicho vector.

$\vec{a} = |\vec{a}| \cdot \vec{u_{a}} = a \cdot \vec{u_{a}}$

Ejemplo

Imagina el vector $\vec{a} = (1, 1)$ . Su módulo es $|\vec{a}| = a = \sqrt{1^{2} + 1^{2}} = \sqrt{2}$ . Pues bien, podemos "inventar" un vector unitario ${\vec{u}}_{a}$ que tenga la misma dirección y sentido que $\vec{a} = (1, 1)$ , y expresar este último según $\vec{a} = \sqrt{2} \cdot {\vec{u}}_{a}$ .

Expresión de un vector mediante su vector unitario

Cuando expresamos un vector cualquiera a partir de su vector unitario, toda la información de dirección y sentido la proporciona dicho vector unitario. La información de tamaño (módulo), la aporta el número (escalar) que multiplica a dicho vector.

En física, los convenios de signos para movimientos en una sola dimensión, por ejemplo, utilizan implícitamente esta idea.

Dedicaremos un apartado a explicarte cómo calcular las coordenadas de dicho vector ${\vec{u}}_{a}$

Puedes utilizar esta simulación de operaciones con vectores para visualizar dinámicamente el efecto que produce la multiplicación de escalares por vectores.

Representación analítica

El producto de un vector $\vec{a}$ por un escalar λ, nos da como resultado otro vector cuyas componentes son el producto de λ por cada una de las componentes del vector $\vec{a}$ .

$λ \cdot \vec{a} = (λ \cdot a_{x}, λ \cdot a_{y}) = (λ \cdot a_{x}) \cdot \vec{i} + (λ \cdot a_{y}) \cdot \vec{j}$

Ejemplos

Si multiplicamos el número 3 por el vector $\vec{a} = (1, 1)$ , nos queda otro vector $\vec{b} = 3 \cdot (1, 1) = (3 \cdot 1, 3 \cdot 1) = (3, 3) = 3 \cdot \vec{i} + 3 \cdot \vec{j}$ . El tamaño del vector ha aumentado, y es tres veces el del vector original $|\vec{b}| = |3| \cdot |\vec{a}| = 3 \cdot \sqrt{2}$ . Su dirección y sentido son iguales a las del vector original.

Si multiplicamos el número -3 por el vector $\vec{a} = (1, 1)$ , nos queda otro vector $\vec{b} = - 3 \cdot (1, 1) = (- 3 \cdot 1, - 3 \cdot 1) = (- 3, - 3) = - 3 \cdot \vec{i} - 3 \cdot \vec{j}$ . El tamaño del vector, de nuevo, ha aumentado, y es tres veces el del vector original $|\vec{b}| = |- 3| \cdot |\vec{a}| = 3 \cdot \sqrt{2}$ . Su dirección es la misma, pero el sentido, en este caso, es el contrario al del vector original.

Si multiplicamos un número menor número 0.5 por el vector $\vec{a} = (1, 1)$ , nos queda otro vector $\vec{b} = 0.5 \cdot (1, 1) = (0.5 \cdot 1, 0.5 \cdot 1) = (0.5, 0.5) = 0.5 \cdot \vec{i} + 0.5 \cdot \vec{j}$ . El tamaño del vector ha disminuido, y es la mitaddel vector original $|\vec{b}| = |0.5| \cdot |\vec{a}| = 0.5 \cdot \sqrt{2}$ . Los tamaños de los vectores siempre disminuyen cuando se multiplican por números que están entre -1 y 1. Su dirección y sentido son iguales a las del vector original.

Como seguro intuyes, no es posible cambiar la dirección de un vector multiplicándolo por un número, aunque sí podemos cambiar su sentido, multiplicándolo por uno negativo.

Vector nulo y vector opuesto

Cuando multiplicamos un vector cualquiera por el número 0, obtenemos el vector nulo.

Se define el vector nulo, o vector cero $\vec{0}$ , como aquel vector de módulo 0 en el que coinciden su origen y su extremo. Por tanto, no tiene dirección. Se obtiene a partir de un vector cualquiera $\vec{v}$

$0 \cdot \vec{v} = \vec{0}$

Cuando multiplicamos un vector cualquiera por -1, obtenemos su vector opuesto.

Dado un vector cualquiera $\vec{v}$ , se define su vector opuesto $- \vec{v}$ como aquel que tiene igual módulo y dirección que el original, pero sentido contrario. Podemos obtenerlo según:

$- 1 \cdot \vec{v} = - \vec{v}$

Vector y su opuesto

El vector opuesto de $\vec{v}$ es otro vector $- \vec{v}$ cuyas componentes son las opuestas a las del vector v. Por ejemplo, si $\vec{v} = (2, - 1) \Rightarrow - \vec{v} = (- 2, 1)$

¿Y la división de un vector entre un número?

Dividir un vector entre un número es, realmente, multiplicarlo por el inverso del número:

$\frac{\vec{v}}{λ} = \frac{1}{λ} \cdot \vec{v}$

Aunque coloquialmente se suele utilizar la expresión "dividir un vector entre un número", no es adecuada desde el punto de vista algebraico.

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.