Masa enlazada en plano inclinado
Enunciado
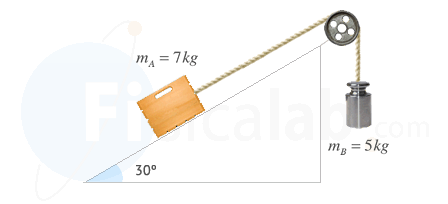
Dado el esquema de la figura, calcular la aceleración de ambas masas sabiendo que el coeficiente de rozamiento cinético es 0.1.
Solución
Datos
mA = 7 kg
mB = 5 kg
μ = 0.1
aA = ?
aB = ?
Resolución
Consideraciones previas
- La cuerda es inextensible y de masa despreciable.
- La polea tiene masa despreciable.
- Como no conocemos el sentido del movimiento, SIEMPRE tendremos que suponer alguno. Aleatoriamente elegiremos que el cuerpo B (la pesa) consigue tirar del cuerpo A (caja) pendiente arriba.
Una vez establecidas las consideraciones anteriores, vamos a estudiar las fuerzas que intervienen en los cuerpos anteriores (diagrama de cuerpo libre).
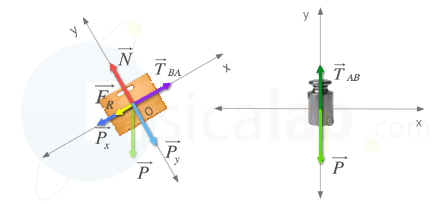
Masa A (Caja)
Las fuerzas que intervienen en la caja durante su ascenso:
- Como hemos supuesto que el cuerpo asciende por el plano, tenemos que tener en cuenta la fuerza de rozamiento (FR), que por definición tiene sentido contrario al movimiento.
- Por otro lado, el cuerpo tendrá su peso (P), que puede descomponerse en dos fuerzas Px y Py que coinciden con el eje de coordenadas.
- La fuerza normal (N).
- La tensión de la cuerda (TBA) que empuja a la caja pendiente arriba.
Aplicando el principio fundamental o segunda ley de Newton, sobre las resultantes de cada eje:
Si trabajamos únicamente con los módulos, daremos valor negativo a las fuerzas que se orientan hacia su semieje negativo y positivo a las que se orienten hacia el semieje positivo, tal y como establece el criterio de signos según los ejes cartesianos que vimos en el apartado Problemas de Fuerzas: Criterios de Signos.
Dado que la caja únicamente se mueve a lo largo del eje x, aAy=0 y aAx=aA
Sustituyendo el valor de N en la primera ecuación, obtenemos que:
Masa B (Pesa)
Las fuerzas que intervienen en la pesa durante su descenso:
- El peso (P) del cuerpo.
- La Tensión de la cuerda (TAB) que evita que el cuerpo caiga libremente por la acción de su peso.
Sabiendo en este caso que únicamente el movimiento y las fuerzas se producen a lo largo del eje y (aBx=0, aBy=aB), si aplicamos la misma metodología que en el cuerpo anterior:
Dado que la cuerda tiene masa despreciable y es inextensible, se cumple que TAB=TBA. Por tanto, sustituyendo la ecuación [2], en la ecuación [1], obtenemos que:
Dado que la cuerda es inextensible y sin masa, el modulo de la aceleración del cuerpo A es el mismo que el módulo de la aceleración del cuerpo B, sin embargo mientras que Aa se orienta hacia el semieje x positivo, aB lo hace hacia el negativo, por lo que aplicando el criterio de signos: aA=-aB.
Por ultimo, si sustituimos los valores para calcular aA, obtenemos que:
A todos los efectos, la intensidad del valor de la aceleración de los cuerpos es el mismo, sin embargo el valor negativo de la aceleración del cuerpo B nos indica que su sentido es el del semieje negativo de sus sistema de referencia.
No hemos encontrado ninguna fórmula destacable en este ejercicio.
