Fuerzas y M.C.U. en Curvas Planas y Curvas Peraltadas
A lo largo de este apartado vamos a estudiar la velocidad y las fuerzas que intervienen en el caso de que un cuerpo de masa m, tome una curva plana (sin ángulo de inclinación) o peraltada (con cierto ángulo de inclinación), ambas de radio R a velocidad constante, es decir, describiendo un movimiento circular uniforme (m.c.u.).
Curva plana
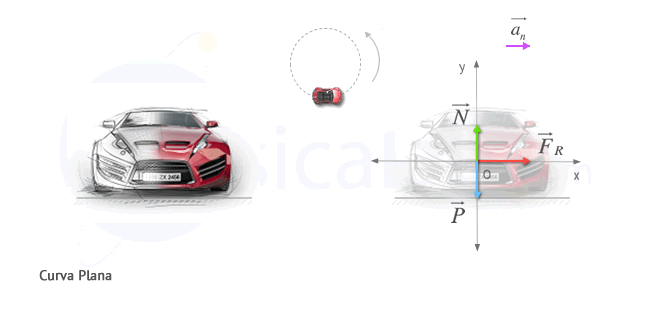
En este caso particular, nos encontramos con las siguientes premisas:
- Como el cuerpo describe un m.c.u., este posee aceleración normal orientada hacia el centro de la curva y por tanto debe sufrir la acción de una fuerza que origine dicha aceleración: la fuerza centrípeta.
- La fuerza centrípeta que obliga a cambiar la dirección del movimiento es la fuerza de rozamiento.
- Adicionalmente en el cuerpo intervienen la fuerza normal y su peso.
Aplicando el principio fundamental o segunda ley de Newton a la resultante de las fuerzas de cada eje de coordenadas, y sabiendo que como no se mueve a lo largo del eje x (ay=0, ax=an), obtenemos que:
Este valor de v, se trata del valor de velocidad máxima que puede alcanzar el cuerpo sin derrapar.
Curva peraltada

Al igual que en el apartado anterior, vamos a analizar el movimiento:
- Es parecido al caso de la curva plana, pero en esta ocasión la curva posee un ángulo A de inclinación.
- Sigue describiéndose un m.c.u. y por tanto, el cuerpo posee aceleración normal y fuerza centrípeta.
- Iguamente siguen interviniendo la fuerza normal, el peso y la fuerza de rozamiento.
- La fuerza normal por definición es perpendicular a la superficie y por tanto, no coincide con el eje de coordenadas, por lo que se puede descomponer en dos fuerzas Nx y Ny.
- La fuerza de rozamiento es perpendicular a la superficie, y por tanto no coincide con nuestro sistema de referencia, por lo que podemos descomponerlo en dos fuerzas FRx y FRy.
- En esta ocasión la fuerza centrípeta es la suma de la fuerza de rozamiento y la fuerza normal en el eje x.
Aplicando la segunda ley de Newton, y sabiendo que como no se mueve a lo largo del eje x (ay=0, ax=an), obtenemos que:
Sustituyendo el valor de N de la segunda ecuación en la primera, y despejando v:
Este valor de v, se trata del valor de velocidad máxima que puede alcanzar el cuerpo sin derrapar.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
