Subir para luego bajar

Datos

α = 30º
v₀ = 4 m/s
m = 2 kg
μ = 0.25

cuestión a)

En primer lugar, vamos a estudiar las fuerzas que intervienen en la caja durante su ascenso:

• Como el cuerpo asciende por el plano, tenemos que tener en cuenta la fuerza de rozamiento (F_R), que por definición tiene sentido contrario al movimiento.
• Por otro lado, el cuerpo tendrá su peso (P), que puede descomponerse en dos fuerzas P_x y P_y que coinciden con el eje de coordenadas.
• La fuerza normal (N).

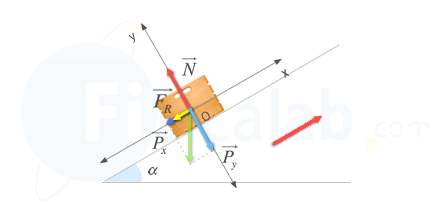
Aplicando el principio fundamental o segunda ley de Newton a la resultante de cada uno de los ejes por separado, obtenemos que:

$$\left.\begin{array}{r}{\sum }_{}{\overrightarrow{F}}_x=m·{\overrightarrow{a}}_x\\ {\sum }_{}{\overrightarrow{F}}_y=m·{\overrightarrow{a}}_y\end{array}\right\}\left.\begin{array}{r}{\overrightarrow{F}}_R+{\overrightarrow{P}}_x=m·{\overrightarrow{a}}_x\\ \overrightarrow{N}+{\overrightarrow{P}}_y=m·{\overrightarrow{a}}_y\end{array}\right\}$$

Si utilizamos únicamente sus módulos y tenemos en cuenta el primero de los criterios de signos estudiados en el apartado de Problemas de Fuerzas: Criterios de Signos, obtenemos que:

$$\left.\begin{array}{r}-F_R-P_x=m·a_x\\ N-P_y=m·a_y\end{array}\right\}$$

Como solo se mueve a lo largo del eje x de nuestro sistema de referencia, a_y = 0 y a_x = a:

$$\begin{gathered} \left.\begin{array}{r}-F_R-P_x=m·a\\ N-P_y=0\end{array}\right\}\left.\Rightarrow \begin{array}{r}-F_R-P_x=m·a\\ N=P_y\end{array}\right\}\Rightarrow \\ \left.\begin{array}{r}-\mu ·N-m·g·\sin \left(\alpha \right)=m·a\\ N=m·g·\cos \left(\alpha \right)\end{array}\right\} \end{gathered}$$

Sustituyendo la fuerza normal obtenida en la segunda ecuación dentro de la primera ecuación, obtenemos que:

$$\begin{gathered} -\mu ·m·g·\cos \left(\alpha \right)-m·g·\sin \left(\alpha \right)=m·a \Rightarrow \\ a=\frac{-\mu ·\cancel{m}·g·\cos \left(\alpha \right)-\cancel{m}·g·\sin \left(\alpha \right)}{\cancel{m}} \Rightarrow \\ a=-0.25·9.8·\cos \left(30\right)-9.8·\sin \left(30\right) \Rightarrow \\ \boxed{a=-7.02 m/s^2} \end{gathered}$$

Durante la subida la velocidad es positiva porque el cuerpo se mueve en el sentido del semieje x positivo, sin embargo la aceleración es negativa (el vector se orienta hacia el semieje x negativo) y provoca que vaya decrementándose hasta detenerse.

cuestión b)

Cuando el cuerpo comienza a descender actúan las mismas fuerzas que en la subida, sin embargo, dado que el movimiento es pendiente abajo, la fuerza de rozamiento cambia de sentido:

$$\left.\begin{array}{r}{\sum }_{}{\overrightarrow{F}}_x=m·{\overrightarrow{a}}_x\\ {\sum }_{}{\overrightarrow{F}}_y=m·{\overrightarrow{a}}_y\end{array}\right\}\left.\begin{array}{r}{\overrightarrow{F}}_R+{\overrightarrow{P}}_x=m·{\overrightarrow{a}}_x\\ \overrightarrow{N}+{\overrightarrow{P}}_y=m·{\overrightarrow{a}}_y\end{array}\right\}$$

$$\left.\begin{array}{r}-P_x+F_R=m·a_x\\ N-P_y=m·a_y\end{array}\right\}$$

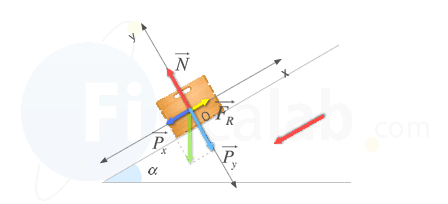
Como solo se mueve a lo largo del eje x de nuestro sistema de referencia, a_y = 0 y a_x = a:

$$\begin{gathered} \left.\begin{array}{r}{F}_R-P_x=m·a\\ N-P_y=0\end{array}\right\}\left.\Rightarrow \begin{array}{r}{F}_R-P_x=m·a\\ N=P_y\end{array}\right\}\Rightarrow \\ \left.\begin{array}{r}\mu ·N-m·g·\sin \left(\alpha \right)=m·a\\ N=m·g·\cos \left(\alpha \right)\end{array}\right\} \end{gathered}$$

Sustituyendo la fuerza normal obtenida en la segunda ecuación dentro de la primera ecuación, obtenemos que:

$$\begin{gathered} \mu ·m·g·\cos \left(\alpha \right)-m·g·\sin \left(\alpha \right)=m·a \Rightarrow \\ a=\frac{\mu ·\cancel{m}·g·\cos \left(\alpha \right)-\cancel{m}·g·\sin \left(\alpha \right)}{\cancel{m}} \Rightarrow \\ a=0.25·9.8·\cos \left(30\right)-9.8·\sin \left(30\right) \Rightarrow \\ \boxed{a=-2.78 m/s^2} \end{gathered}$$

En este caso, la velocidad será negativa porque la caja se mueve en el sentido del semieje negativo, y la aceleración sigue siendo negativa, provocando que la velocidad vaya aumentando su valor en ese sentido.