Fuerzas en Planos Inclinados

Si a un cuerpo le aplicamos una fuerza paralela a su vector velocidad, que además sea constante en módulo, dirección y sentido, conseguiremos que este experimente un movimiento rectilíneo uniformemente variado (m.r.u.v.). Si además, el cuerpo estaba en reposo, el movimiento se producirá en la dirección y sentido de dicha fuerza.

Movimientos en un Plano Inclinado

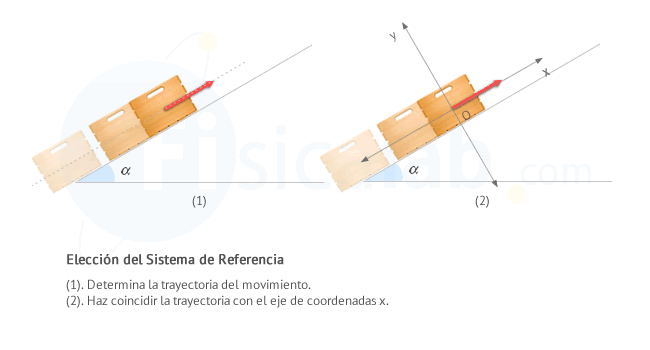
Cuando un cuerpo se desliza por un plano inclinado, con un ángulo de inclinación α, mediante un m.r.u.a. descendiendo o ascendiendo, el sistema de referencia más útil que podemos utilizar es aquel en el que hacemos coincidir el eje x con la trayectoria en línea recta que sigue el cuerpo sobre el plano. Al hacer esto, conseguimos que el cuerpo:

• Se mueva a lo largo del eje X, por lo que dado que se trata de un m.r.u.a, su aceleración a lo largo de este eje será a_x = a.
• No se mueva a lo largo del eje Y, por lo que su aceleración será a_y = 0.

Por tanto, si aplicamos la segunda ley de Newton en cada eje se cumple que:

$${\sum }_{}{F}_x=m·a ⋮ {\sum }_{}{F}_y=0$$

Si trabajas únicamente con los módulos, al calcular la fuerza resultante, recuerda que debes seguir alguno de los criterios de signos que estudiamos en el apartado Problemas de Fuerzas: Criterios de Signos