Fuerzas y Movimientos Verticales
Si a un cuerpo le aplicamos una fuerza paralela a su vector velocidad, que además sea constante en módulo, dirección y sentido, conseguiremos que este experimente un movimiento rectilíneo uniformemente variado (m.r.u.v.). Si además, el cuerpo estaba en reposo, el movimiento se producirá en la dirección y sentido de dicha fuerza.
Movimientos Verticales
Cuando un cuerpo se mueve verticalmente mediante un m.r.u.a. de forma ascendente o descendente, el sistema de referencia más útil que podemos utilizar es aquel en el que hacemos coincidir uno de los ejes con la trayectoria en línea recta que sigue el cuerpo. Al hacer esto, conseguimos que el cuerpo:
- No se mueva a lo largo del eje X, por lo que su aceleración a lo largo de este eje es nula. ax = 0
- Se mueva a lo largo del eje Y, por lo que dado que se trata de un m.r.u.a, su aceleración será ay = a.
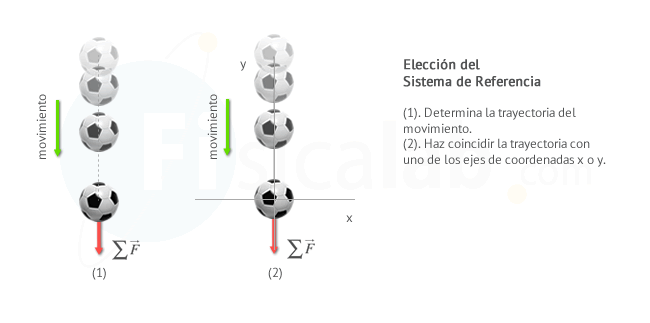
Por tanto, si aplicamos la segunda ley de Newton en cada eje se cumple que:
Si trabajas únicamente con los módulos, al calcular la fuerza resultante, recuerda que debes seguir alguno de los criterios de signos que estudiamos en el apartado Problemas de Fuerzas: Criterios de Signos
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
