Fuerzas y M.C.U. en un Plano Vertical
Un ejemplo clásico de la dinámica del movimiento circular uniforme (m.c.u.), es el que se produce cuando tenemos un cuerpo de masa m atado a una cuerda de longitud l que hacemos girar en un plano vertical con una velocidad v. A lo largo de este apartado, vamos a estudiar las fuerzas que intervienen en este caso específico.
En concreto, la resultante de las fuerzas que actúan sobre el cuerpo es:
Si estudiamos las fuerzas que intervienen en el punto más alto (A) y más bajo (B) de la trayectoria, obtendremos las siguientes conclusiones:
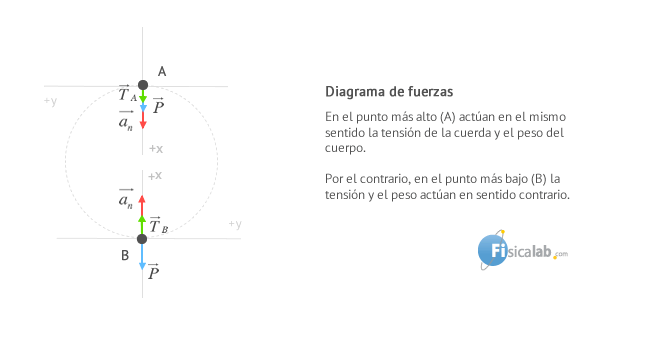
Punto más alto (A)
Considerando el sistema de referencia intrínseco comentado en el apartado de la fuerza centrípeta, obtenemos que:
Punto más bajo (B)
Estudiando la fuerza resultante en el sistema de referencia elegido, obtenemos que:
¿Cuál es la velocidad mínima para que no caiga el cuerpo?
El cuerpo no caerá mientras que el valor de la Tensión de la cuerda TA en el punto más alto no sea inferior a 0 N. Por tanto, la velocidad mínima que puede tener al cuerpo sin caer será aquella en la que TA=0 N. Sustituyendo en la ecuación de este punto:
¿Cuál es la velocidad máxima sin que se rompa la cuerda?
Si llamamos, TMax a la máxima tensión que es capaz de soportar la cuerda, esta se producirá en el punto más bajo del movimiento, ya que es ahí donde la cuerda sufre más. Por tanto, si lo sustituimos en su ecuación:
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
