Masas enlazadas

Resolución

Antes de realizar ningún cálculo, debemos obtener el diagrama de cuerpo libre de cada peso.

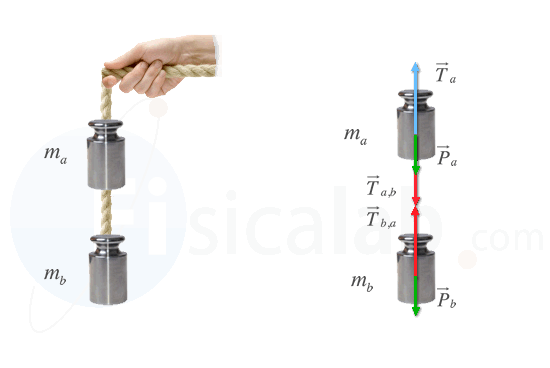
Aplicando la segunda ley de Newton a cada cuerpo por separado obtenemos que:

masa a

$$\begin{gathered} {\sum }_{}{\overrightarrow{F}}_a=m_a·\overrightarrow{a} \Rightarrow \\ {\overrightarrow{T}}_a+{\overrightarrow{T}}_{a,b}+{\overrightarrow{P}}_a = m_a·\overrightarrow{a} \end{gathered}$$

Si consideramos únicamente sus módulos, T_a,b y P_a tiran en sentido contrario a T_a, por lo que:

$$\begin{gathered} T_a-T_{a,b}-P_a = m_a·a \Rightarrow \\ T_a-T_{a,b}-m_a·g = m_a·a \Rightarrow \\ T_a-T_{a,b} = m_a · (a+g) \end{gathered}$$

Como las cuerdas son inextensibles y carente de masa, la tensión es igual en todos sus puntos, por lo que T_a,b=T_b,a. Para simplificar, a estas dos tensiones las llamaremos simplemente T_b.

$$T_a-T_b = m_a · (a+g)$$

masa b

En el caso de esta masa, si aplicamos la segunda ley de Newton:

$$\begin{gathered} {\sum }_{}{\overrightarrow{F}}_b=m_b·a \Rightarrow \\ {\overrightarrow{T}}_b+{\overrightarrow{P}}_b = m_b·a \Rightarrow \\ {T}_b-m_b·g=m_b·a \Rightarrow \\ {T}_b = m_b·(a+g) \end{gathered}$$

Sustituyendo este valor en la expresión de la masa a, obtenemos que:

$$\boxed{T_a = (m_b+m_a)·(a+g) ⋮ T_b = m_b·(a+g)}$$