Masas en contacto
Enunciado
Dado el esquema de la figura determina las fuerzas que actúan sobre cada una de las cajas que se muestran y calcula las aceleración que adquieren cada una de ellas.
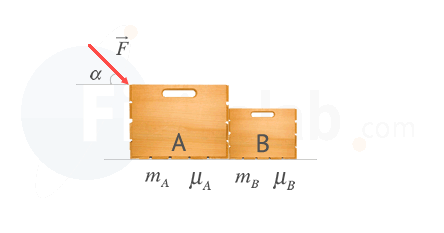
Solución
En el cuerpo A intervienen las siguientes fuerzas:
- la fuerza F que se aplica sobre A en la parte superior y que es equivalente a aplicarla con la misma dirección y sentido desde su centro. Esta se puede descomponer en dos fuerzas Fx y Fy para que coincidan con la dirección de los ejes de coordenadas.
- Como A empuja a B, por el principio de acción reacción B ejercerá sobre A una fuerza de reacción que llamaremos FBA.
- La fuerza normal (NA)
- El peso del cuerpo (PA)
- La fuerza de rozamiento (FRA)
Por otro lado en el cuerpo B se aplican:
- La fuerza que ejerce la caja A sobre B y que llamaremos FAB.
- Su fuerza normal (NB)
- El peso de la caja B (PB)
- La fuerza de rozamiento con el suelo (FRB)
Si dibujamos el diagrama de cuerpo libre de cada caja, obtendremos lo siguiente:
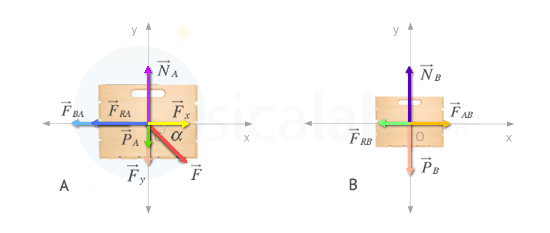
Vamos a estudiar independientemente cada una de las cajas.
Caja A
Si aplicamos la segunda ley de newton a la resultante de cada uno de los ejes del sistema de referencia, obtenemos que:
Aplicando la definición de resultante:
En vez de utilizar vectores, vamos a emplear sus módulos para realizar los cálculos más cómodamente. En este caso, siguiendo el primero de los criterios del apartado Problemas de Fuerzas: Criterios de Signos :
Como el movimiento se realiza en horizontal aAy=0 y aAx=aA. Además si sustituimos los valores de Fx, Fy y la fuerza de rozamiento:
Sustituyendo el valor de NA de la segunda ecuación en la primera, tenemos que:
Caja B
Aplicando la misma metodología que en la caja A, obtenemos que para el caso de la caja B:
Sustituyendo:
Por último, sustituyendo la segunda ecuación en la primera, nos queda:
Como finalmente las dos cajas se mueven a la vez, se cumple que aA=aB=a. Además, como FAB y FBA son fuerzas de acción reacción, se cumple que FAB=FBA. Por tanto, si sumamos las ecuaciones [1] y [2]:
No hemos encontrado ninguna fórmula destacable en este ejercicio.
