Gravedad y Movimiento Planetario
El movimiento de los planetas alrededor del Sol se debe fundamentalmente a la fuerza de la gravedad. Mercurio, Venus, la Tierra o Júpiter son algunos ejemplos de planetas que giran en torno al Sol. Cada uno cuenta con su propia órbita y características pero en todos los casos esta está determinada por la ley de gravitación. En este apartado vamos a estudiar algunas propiedades y magnitudes de la fuerza gravitatoria que son la causa última de tales órbitas. Haremos un enfoque dinámico, es decir, basado en la propia fuerza. Si deseas un enfoque energético, más adelante te explicaremos cómo influye la energía del cuerpo en las órbitas planetarias.
A continuación veremos:
- La fuerza de gravedad como una fuerza central
- Su momento
- La variación temporal del momento angular
- Cómo influyen estas magnitudes en las órbitas
En todos los casos consideraremos el planeta y el Sol como partículas puntuales. Recuerda que podemos hacer dicha aproximación siempre que las trayectorias descritas por los cuerpos sean mucho mayores que sus dimensiones.
La gravedad es una fuerza central
Tal y como hemos visto en niveles anteriores, decimos que una fuerza es central cuando siempre se dirige al mismo punto, independientemente del movimiento que tenga el cuerpo y cuando su valor depende exclusivamente de la distancia del cuerpo a dicho punto. Lo cierto es que la fuerza gravitatoria que ejerce el Sol sobre un planeta, independientemente de cómo sea la órbita de este, se dirige siempre desde el planeta hacia el propio Sol y su valor es inversamente proporcional a la distancia entre ellos. Esto es,
La fuerza gravitatoria que ejerce el Sol sobre los planetas es una fuerza central dirigida siempre hacia el propio Sol y cuyo valor es inversamente proporcional al cuadrado de la distancia entre este y el planeta. Esto se cumple tanto si la órbita es circular como si la órbita es elíptica.
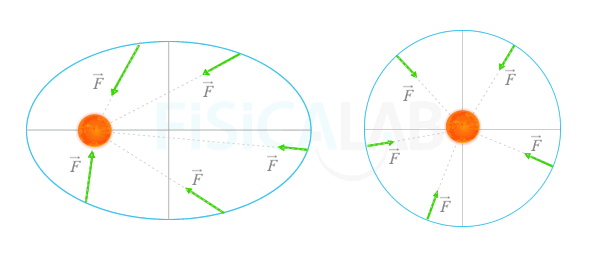
Fuerza central
Desde el punto de vista energético las implicaciones son claras: ya sabemos, dado que las fuerzas centrales son fuerzas conservativas, que el trabajo que realizan a lo largo de un camino cerrado, como es la órbita de un planeta, es cero. Es decir, los planetas mantienen su energía constante en su recorrido espacial alrededor del Sol.
Momento de la fuerza gravitatoria
También conocemos de apartados anteriores la importancia que tiene el momento de un vector en el estudio dinámico de los cuerpos que giran. Lo habíamos estudiado en el contexto del sólido rígido pero podemos llegar a conclusiones similares en el caso de planetas que giran entorno al Sol por efecto de la ley de la gravedad.
El momento de la fuerza gravitatoria que actúa en un planeta que gira en torno al Sol, respecto al propio Sol es siempre cero.
El enunciado anterior se cumple para cualquier fuerza central. Efectivamente, como puede comprobarse en la figura inferior:
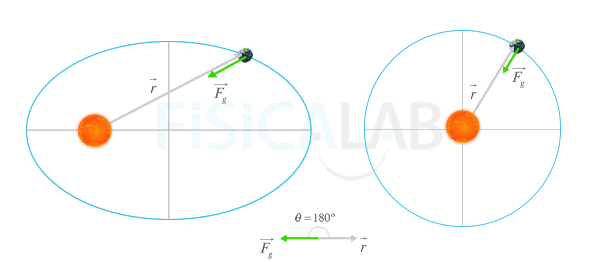
Fuerza y Posición tienen sentidos opuestos
Recuerda que, en Física, cuando ejercemos un momento de fuerza sobre un cuerpo modificamos su estado de giro o rotación. Dado que el momento de la fuerza gravitatoria es cero, podemos concluir que el estado de rotación permanece constante.
Momento angular
Desde el punto de vista de la dinámica existen dos magnitudes fuertemente relacionadas que se suelen usar para caracterizar el comportamiento de los cuerpos.
- El momento lineal
- El momento angular
Para determinar como varía el momento angular en el tiempo derivamos respecto a t
Observa que
El producto
En el caso concreto de la fuerza gravitatoria que actúa sobre un planeta, hemos visto que su momento es cero, por lo que podemos escribir:
El momento angular de un planeta que se mueve bajo la acción de la fuerza gravitatoria se mantiene constante en módulo, dirección y sentido.
La afirmación anterior, que es válida para cualquier cuerpo que se mueva bajo la acción de fuerzas centrales, queda reflejada en la siguiente imagen.
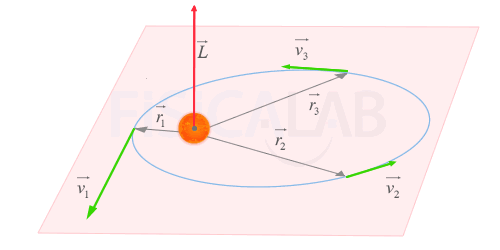
Órbita plana y velocidad aerolar constante
El producto vectorial
Consecuencias para las órbitas
Las principal conclusión a la que hemos llegado en relación a la fuerza gravitatoria, como fuerza central, es que el momento angular de cualquier planeta que gira en torno al Sol se mantiene constante. Esto implica que:
- Para que la dirección y el sentido del momento angular sea constante, las órbitas deben estar contenidas en un plano (al cual el momento es perpendicular, como se apreciaba en la imagen anterior)
- Para que su módulo sea constante podemos distinguir dos casos:
-
Si la órbita del planeta es circular, la velocidad será constante, ya que la masa m y el radio r también lo son. En este caso, en el que además
- Si la órbita es elíptica…
-
...la velocidad instantánea del planeta varía continuamente, tal y como predecía la ley de las áreas de Kepler:
-
...la velocidad areolar vA, esto es, el área recorrida por unidad de tiempo, permanece constante:
Donde hemos aplicado:
-
-
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.

