Intensidad del Campo Gravitatorio
La intensidad del campo gravitatorio es, junto con el potencial gravitatorio, la magnitud que se utiliza para cuantificar el campo gravitatorio en un punto. A diferencia del potencial, la intensidad de campo es una magnitud vectorial. Como vamos a ver, es una magnitud útil para estudiar las fuerzas que aparecen en un cuerpo fruto de la acción gravitatoria, en contraste con el potencial, que es útil para estudiar la energía potencial que posee. En este apartado veremos:
- El concepto de intensidad del campo gravitatorio
- La expresión del campo gravitatorio creado por una masa puntual y sus propiedades
- Las características del campo gravitatorio que crean los cuerpos esféricos
- La intensidad del campo gravitatorio creado por varias masas
- Cómo representar gráficamente la intensidad de campo
¿Preparado?
Concepto de intensidad de campo gravitatorio
La intensidad del campo gravitatorio (
La unidad de intensidad del campo gravitatorio en el Sistema Internacional (S.I.) es el newton por kilogramo (N/kg).
Así, conocido el campo gravitatorio en un punto, podemos calcular la fuerza gravitatoria que experimentará una masa cualquiera m en dicho punto según:
Observa que la intensidad de campo gravitatorio es la magnitud que define al campo desde un punto de vista dinámico, es decir, de las fuerzas que actúan sobre los cuerpos. Por otro lado, observa la similitud que guarda la expresión anterior con la segunda ley de Newton. No es casual que la unidad de medida para el campo gravitatorio (o intensidad de campo gravitatorio) coincida con la unidades de medida de la aceleración: N/kg = m/s2. De ahí que, en ocasiones, a
Intensidad de campo creada por una masa puntual
Tal y como hemos visto anteriormente, en el caso de que deseemos calcular la intensidad del campo gravitatorio en un determinado punto creado por una única masa puntual m, deberemos introducir una masa testigo m' en dicho punto. A partir de aquí podemos emplear la expresión de la fuerza gravitatoria (para calcular la fuerza que experimenta m') y la definición de intensidad del campo en un punto:
La intensidad del campo gravitatorio generado por una masa puntual en un punto se puede calcular mediante la siguiente expresión:
Donde:
- G : Es la constante de gravitación universal. Su valor es G = 6.67·10-11 N·m2/kg2
- m : Masa del cuerpo que genera el campo. Su unidad de mediada en el Sistema Internacional (S.I.) es el kilogramo (kg)
- r : Es el módulo del vector
Observa que cuando dejamos un cuerpo en el seno de un campo gravitatorio, este tenderá a moverse en el mismo sentido del campo (si no existen más fuerzas actuando sobre él) ya que la fuerza gravitatoria que aparece, y por tanto, la aceleración, tendrán igual sentido que
En la siguiente imagen puedes distinguir los elementos que intervienen en el campo gravitatorio:
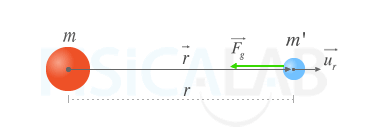
Campo gravitatorio generado por una masa puntual
Si situamos una masa en el espacio, esta "perturba" el entorno que le rodea. Si posteriormente situamos una masa testigo m', esta experimentará una fuerza gravitatoria que la impulsará a moverse en el mismo sentido del campo. Podemos explicar dicha fuerza como fruto de la interacción de la masa testigo con el campo.
Propiedades
El vector intensidad de campo gravitatorio creado por una masa puntual tiene las siguientes propiedades:
- Su sentido se orienta hacia la masa que genera el campo, tal y como indica el signo - de la expresión
- Depende de la masa que lo crea y es independiente de la masa o masas a las que pueda afectar
- Su valor se reduce con el cuadrado de la distancia, siendo es el mismo para todas las partículas que se sitúan a una determinada distancia de la masa generadora. Dicho con otras palabras: tiene simetría esférica
- Tiene dirección radial, como indica el vector
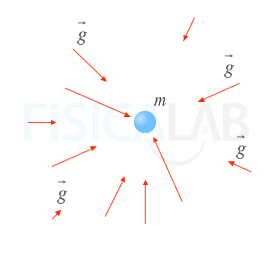
Propiedades de la intensidad de campo gravitatorio
Las flechas rojas de la figura representan el valor del campo gravitatorio en distintos puntos del espacio. Las flechas que están a igual distancia del centro tienen el mismo módulo (simetría esférica) y apuntan hacia la partícula generadora (dirección radial).
Intensidad de campo creado por una esfera
Lo cierto es que en el mundo real no existen partículas puntuales sino cuerpos con simetría esférica que, según las circunstancias, podemos considerar partículas puntuales. Sin embargo, los resultados obtenidos para el caso de las esferas son muy similares a los ya estudiados. Consideraremos un cuerpo esférico de masa m y distinguiremos varios casos:
-
Corteza esférica homogénea: Se trata de un cuerpo esférico hueco cuya masa se encuentra distribuida de manera uniforme en la capa más superficial.
-
Campo en el exterior: La intensidad del campo gravitatorio en un punto P cualquiera del exterior de una corteza esférica a una distancia r de su centro es el mismo que el que originaría una partícula puntual situada en el centro de la esfera:
-
Campo en el interior: La intensidad del campo gravitatorio en un punto P cualquiera del interior de una corteza esférica es nulo.
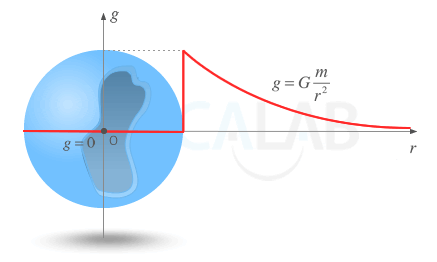
Variación del valor del campo gravitatorio en una corteza esférica
-
-
Esfera sólida homogénea: Se trata de un cuerpo macizo con forma esférica cuya masa se encuentra distribuida de manera uniforme a lo largo de todo su volumen. Se puede considerar desde el punto de vista teórico como una sucesión de infinitas cortezas esféricas de distinto tamaño unas encajadas en las otras.
-
Campo en el exterior: La intensidad del campo gravitatorio en un punto P cualquiera del exterior de una esfera sólida a una distancia r de su centro es el mismo que el que originaría una partícula puntual situada en el centro de la esfera:
-
Campo en el interior: La intensidad del campo gravitatorio en un punto P del interior de la esfera sólida situado a una distancia r' del centro varía linealmente conforme a r':
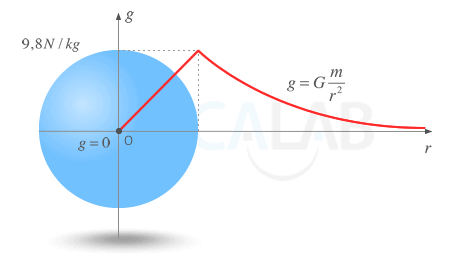
Variación del valor del campo gravitatorio en una esfera sólida
-
Intensidad de campo creada por varias masas
Cuando queremos calcular el campo generado por varias masas, ya sean estas puntuales o no, podemos aplicar el principio de superposición.
La intensidad del campo gravitatorio de un sistema de n masas en un punto se calcula sumando vectorialmente los campos individuales que produce cada una de las masas individuales en dicho punto:
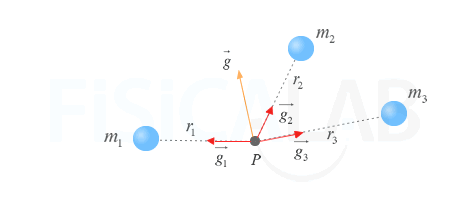
Intensidad de campo gravitatorio creado por varias masas
Podemos obtener el campo gravitatorio generado por un conjunto de partículas en un punto sumando las contribuciones de cada uno de los campos que crea cada partícula por si sola.
Líneas de fuerza
Las líneas de fuerza, también denominadas líneas de campo, nos permiten visualizar la forma en que se distribuye la intensidad del campo gravitatorio en el espacio. Ten en cuenta las siguientes propiedades si debes trazarlas:
- Se trata de líneas contínuas
- En cuanto a la dirección, son tangentes en cada punto al vector intensidad de campo gravitatorio
- En cuanto al sentido, es siempre entrante hacia la masa generadora de campo. Coincide, por tanto, con el sentido del vector intensidad del campo gravitatorio. Representaremos el sentido mediante una flecha situada sobre la linea
- En cuanto a su extensión, cada línea partiría idealmente desde el infinito y moriría en el punto en el que se genera el campo. Es decir, abarca toda la extensión abarcada por el campo
- En cuanto a su cantidad, el número de líneas que atraviesan una unidad de superficie es proporcional al módulo de la intensidad de campo
- Nunca se entrecruzan
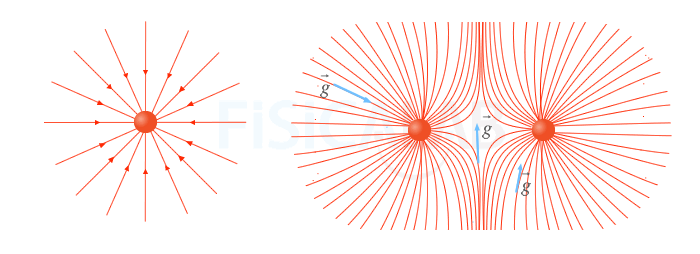
Líneas de campo gravitatorio
Las líneas de campo de la figura representan el campo gravitatorio originado por una masa puntual y por dos masas puntuales respectivamente. En el caso de las dos masas puntuales, observa como el vector intensidad de campo, en azul es tangente en cada punto a la linea sobre la que se dibuja.
Si lo deseas puedes ampliar información sobre otras formas de representar el campo gravitatorio.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
