Energía Potencial Gravitatoria
Podemos entender la energía de los cuerpos como la capacidad que tienen de producir un trabajo.
Definimos la energía potencial como aquella que poseen los cuerpos por el hecho de encontrarse en una determinada posición en un campo de fuerzas.
La fuerza gravitatoria es una fuerza central y, por tanto, conservativa. Sólo las fuerzas conservativas dan lugar a energía potencial. Efectivamente, cuando realizamos un trabajo para vencer una fuerza conservativa, este no se pierde, sino que queda almacenado de forma latente, de forma potencial, pudiendo ser devuelto posteriormente. Dicho de otro modo: el trabajo realizado contra la fuerza conservativa equivale a una transferencia de energía que queda almacenada de algún modo, esto es, en modo de energía potencial.
En este apartado vamos a profundizar en el estudio de la energía potencial gravitatoria, es decir, la que origina la fuerza gravitatoria. Esto nos permite estudiar la ley de la gravedad desde un punto de vista energético. A partir de ahí, podremos definir, en apartados posteriores, el potencial gravitatorio, magnitud que, junto a la intensidad de campo, nos permite cuantificar los campos gravitatorios. Si lo que deseas es tener una primera aproximación al concepto de energía potencial gravitatoria, puedes pulsar sobre la pestaña Ver también en la parte superior de la página donde encontrarás el enlace correspondiente.
Trabajo realizado por las fuerzas conservativas
Cuando un cuerpo realiza un trabajo, está, de un modo u otro, variando su energía. Recordemos que, al fin y al cabo, podemos decir que la energía que tiene un cuerpo es la capacidad que tiene para realizar un trabajo. En el caso de las fuerzas conservativas, podemos encontrar una relación entre el trabajo que realizan y la energía potencial.
El trabajo que realizan las fuerzas conservativas, incluida la fuerza de gravedad, se puede calcular como la variación negativa de la energía potencial del sistema.
La expresión anterior nos permite calcular el trabajo que realiza una fuerza conservativa cuando un cuerpo se desplaza desde una posición inicial a una posición final a partir de una simple resta. En apartados anteriores hemos calculado el valor del trabajo realizado por la fuerza gravitatoria mediante integrales, con lo cual parece que las cosas se nos han simplificado bastante...
Sin embargo, la expresión define la energía potencial como un valor relativo, se trata de un incremento. ¿Cómo podemos calcular el valor de la energía potencial en un punto concreto?
Calculando la energía potencial gravitatoria
La expresión anterior determina que la energía potencial es siempre un valor relativo respecto a otro. Por ello, para poder determinar la energía potencial en un punto de manera absoluta debemos fijar un valor cero de energía potencial que nos sirva de referencia.
Fijaremos el valor cero de energía potencial gravitatoria aquel en el que la fuerza gravitatoria es cero, es decir, el valor cero de energía potencial se sitúa en el infinito.
Para calcular la energía potencial asociada a una posición rA cualquiera, utilizaremos una masa M generadora de campo situada en el centro de nuestro sistema de referencia y una masa testigo m.
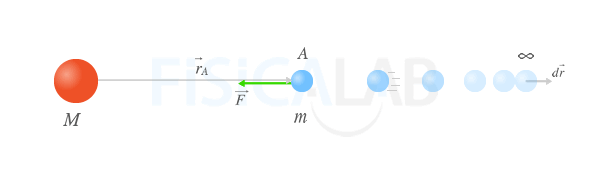
Cálculo de la Energía Potencial Gravitatoria
Sistema de dos masas del que nos valemos para calcular el trabajo realizado por el campo gravitatorio para llevar una partícula desde el infinito al punto genérico A
Calculemos el trabajo que realiza la fuerza gravitatoria para llevar la masa m desde el infinito hasta el punto A:
Si consideramos, como hemos dicho,
Podemos extender el desarrollo anterior para una posición genérica r.
La energía potencial gravitatoria
Donde:
- G es la constante de gravitación universal, que no depende de los cuerpos que interaccionan y cuyo valor es G = 6,67·10-11 N·m2/kg2
- M y m son las masas de las partículas del sistema. Su unidad de medida en el Sistema Internacional es el kilogramo (kg)
- r es la distancia que las separa. Su unidad de medida en el Sistema Internacional (S.I.) es el metro
En ocasiones también podrás encontrar definida la energía potencial gravitatoria como menos el trabajo que realiza el campo gravitatorio para llevar la masa m desde el infinito hasta la citada distancia r. Por tanto, nos da una medida del trabajo que sería necesario hacer para separar una distancia infinita ambas masas.
La expresión anterior es válida para cualquier sistema que esté formado por dos partículas puntuales, pero también cuando, aun no siendo partículas puntuales, sean cuerpos con simetría esférica (esfera homogénea, con capas concéntricas o hueca). Observa también que si m tiene una determinada energía potencial debida a M cuando se encuentran separadas una distancia r, M tendrá la misma energía potencial debida a m, por lo que en ocasiones se habla de la energía del sistema, en lugar de la energía de m o de M.

Energía potencial y la simetría esférica
Podemos aplicar la expresión
Características
A partir de la expresión de energía potencial gravitatoria podemos deducir las siguientes propiedades:
- Siempre es negativa. El valor máximo que puede tomar es 0, y esto ocurre cuando las masas están infinitamente lejos. A medida que las masas se acercan, la capacidad para desarrollar un trabajo, si se dejaran libres, disminuye. Por ello, la energía potencial gravitatoria debe ser menor en cualquier punto genérico del espacio que en el infinito, es decir, debe ser negativa
- Cuando dos masas se acercan, disminuye la energía potencial. Cuando dos masas se alejan aumenta la energía potencial
-
El trabajo exterior mínimo necesario para alejar o acercar dos masas se calcula a partir de la variación de energía potencial, según
-
Su gráfica, en función de la distancia, es la siguiente
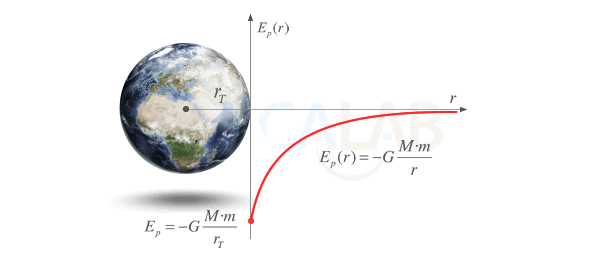
Energía potencial gravitatoria cercano a la Tierra
A medida que alejamos una masa genérica m de la Tierra, de masa M, el trabajo capaz de desarrollar la fuerza de la gravedad sobre ella aumenta, al aumentar también la distancia de separación. Esta capacidad de desarrollar un trabajo es lo que cuantificamos mediante la energía potencial gravitatoria y ocurriría si la masa m quedase libre a una distancia r bajo único efecto de la gravedad.
Si deseas ampliar información sobre las gráficas propias del campo gravitatorio visita "Representación Gráfica del Campo Gravitatorio"
-
Por otro lado, cuando la distancia es infinita, el trabajo es 0 ya que la masa m sería incapaz de sentir los efectos de la fuerza gravitatoria de la Tierra.
Valor m·g·h
Puede que estés acostumbrado a usar el valor Ep = m·g·h. En niveles anteriores, cuando hicimos la introducción a la energía potencial gravitatoria, así lo hacíamos. Vamos a comprobar que dicho valor es un caso particular que podremos usar cuando nos encontremos a una cierta altura h no muy grande sobre la superficie terrestre, es decir, cerca del suelo. La energía potencial de un cuerpo de masa m sobre la superficie de la Tierra, de masa M y radio rT viene dada por:
Si situamos el cuerpo a cierta altura h sobre la superficie ( r = rT + h ), la energía potencial gravitatoria es:
La variación de energía potencial entre ambos puntos:
Ahora bien, sabemos que rT >> h, por lo que podemos despreciar rT·h frente a rT2. También sabemos que, en la superficie terrestre, g = G·M/rT2. Con esto podemos escribir:
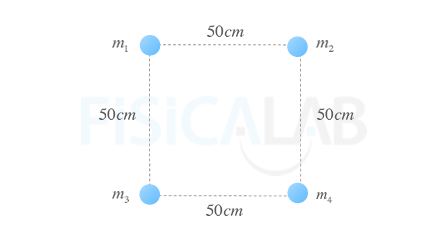
Sistema de varias partículas
El razonamiento utilizado en un sistema de dos partículas es válido también cuando tenemos tres o más.
La energía potencial gravitatoria de un sistema de tres o más partículas nos da la medida del trabajo que sería necesario para separarlas haciendo infinita la distancia entre las mismas. Se calcula sumando la que posee cada par de partículas.
La expresión anterior permite el cálculo de la energía potencial del sistema, es decir, del conjunto de partículas. Dicho valor será en general distinto al que tenga cada partícula individual del sistema, tal y como se ilustra en este ejercicio. Finalmente, observa que para su cálculo no debes contar dos veces la misma pareja, esto es, Ep(2,3) = Ep(3,2), por ejemplo.Recuerda que el número de términos que contiene el sumario se puede calcular a partir del número de combinaciones que pueden formarse con n elementos tomados de dos en dos:
Y ahora... ¡Ponte a prueba!
Apartados relacionados
Este mismo apartado se encuentra desarrollado en otros niveles educativos. Si sus contenidos no se ajustan al nivel que buscas, prueba a visitar: