Consideraciones Energéticas Adicionales del Campo Gravitatorio

Estudiar el campo gravitatorio desde un punto de vista energético, aunque pueda resultar algo más abstracto al principio, nos permite simplificar enormemente algunos cálculos de gran relevancia, como por ejemplo saber qué velocidad debe tener un cuerpo para escapar de la influencia de la Tierra. En este apartado veremos:

El teorema de conservación de la energía mecánica aplicado a cuerpos que se mueven exclusivamente bajo la acción de la fuerza gravitatoria
La velocidad de escape de un cuerpo asociado a un campo gravitatorio producido por otro
El concepto de cuerpo libre y ligado a un campo, sus gráficas y su influencia en las órbitas de los planetas

Para ello te recomendamos que estés familiarizado con el concepto de energía potencial gravitatoria que hemos tratado previamente. ¿Empezamos?

Conservación de la energía mecánica

En el caso de un cuerpo que se encuentre inmerso en un campo gravitatorio, su energía mecánica es la suma de su energía cinética, asociada a la velocidad del movimiento, y la energía potencial, asociada a su posición en el campo gravitatorio. El hecho de que las órbitas planetarias sean constantes nos permite intuir que la energía mecánica de los planetas y satélites se mantiene también constante. Efectivamente, la fuerza gravitatoria es una fuerza conservativa y por tanto, la variación de energía mecánica en un cuerpo sometido exclusivamente a la fuerza gravitatoria es cero:

$∆ E_{m} = 0 \Rightarrow ∆ E_{m} = ∆ E_{c} + ∆ E_{p} = 0$

Podemos comprobar la afirmación anterior a partir de los siguientes puntos:

El trabajo realizado por la fuerza gravitatoria cuando el cuerpo sobre el que actúa se desplaza entre dos puntos viene dado, como fuerza conservativa que es, por la variación negativa de su energía potencial gravitatoria:

$W_{g} = - ∆ E_{p}$
El trabajo realizado por la fuerza total, que en este caso coincide con la gravitatoria, cuando el cuerpo se desplaza entre dos puntos coincide, según el teorema de la energía cinética, con la variación de energía cinética experimentada por el cuerpo:

$W_{g} = ∆ E_{c}$

Con lo que nos quedaría:

$\begin{array}{r} W_{g} = - ∆ E_{p} \\ W_{g} = ∆ E_{c} \end{array}\} - ∆ E_{p} = ∆ E_{c} \Rightarrow ∆ E_{c} + ∆ E_{p} = 0 \Rightarrow ∆ E_{m} = 0$

Esto implica que:

En órbitas elípticas la energía potencial es menor en los puntos más cercanos al foco y por tanto la energía cinética (la velocidad del cuerpo) deberá ser mayor. La razón podemos encontrarla en la siguiente figura

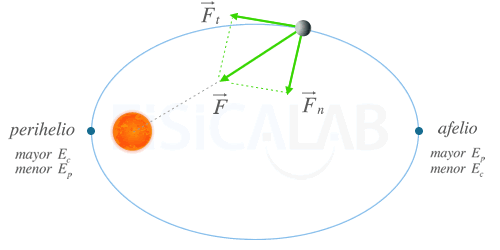
Energía mecánica en órbitas elípticas

La existencia de una componente tangencial en la fuerza gravitatoria de órbitas elípticas hace que la energía cinética y la potencial varíen a lo largo de la misma, aunque su suma, la energía mecánica, permanece constante.
El trabajo necesario para que dicha variación ocurra es realizado precisamente por la componente tangencial de la fuerza gravitatoria ya que la componente normal es perpendicular al desplazamiento.
En órbitas circulares la energía potencial y la energía cinética permanecen constantes. La razón, de nuevo, podemos encontrarla en la siguiente figura

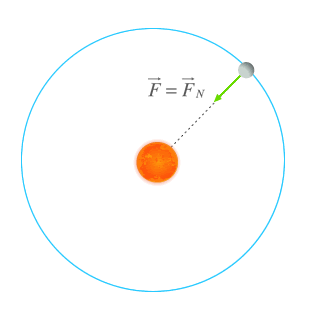
Energía mecánica en órbitas circulares

En órbitas circulares la fuerza gravitatoria es siempre normal a la trayectoria por lo que la energía cinética y la potencial permanecen inalteradas.
Puedes comprobar de manera interactiva cómo varía la velocidad de los planetas en órbitas elípticas en la sección experimenta y aprende que incluimos en el apartado de gravedad y movimiento planetario.

Velocidad de escape

¿Has pensado alguna vez qué velocidad tendrías que imprimir a un balón para que se alejase de la Tierra y no volviese jamás? Vamos a tratar de responder a esta pregunta desde la óptica de la Física.

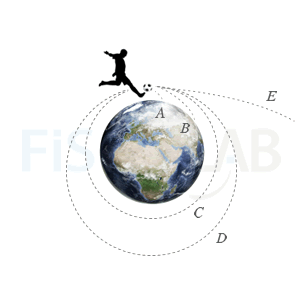
Trayectorias que sigue un balón lanzado desde la Tierra con distintas fuerzas.

Velocidad de escape

Desde la cima de una montaña un super hombre de gran fuerza chuta balones con cada vez más velocidad. Los balones A y B caen en Tierra. El C y el D entran en órbita, circular y elíptica respectivamente. El E escapa a la acción del campo generado por la Tierra. ¿A qué velocidad salió disparado?

Sabemos que el campo gravitatorio generado por la Tierra deja de tener efectos a una distancia infinita de la misma. Así, un cuerpo como el balón de la figura, que se sitúa a una distancia infinita de la Tierra no experimentará la fuerza gravitatoria que ocasiona al ser esta inversamente proporcional al cuadrado de la distancia.

Podemos buscar cual es la velocidad inicial, es decir, la energía cinética, que sería necesario que tuviera el cuerpo, situado inicialmente en la superficie, para que escapase de la atracción de la Tierra. A dicha velocidad la llamaremos velocidad de escape y para llegar a ella seguiremos un enfoque energético. Tendremos en cuenta:

Que situar un cuerpo en el infinito significa conferirle una energía potencial E_p= 0 ( la energía potencial gravitatoria, recordamos, es cero en el infinito y negativa a cualquier distancia genérica r )
Que para conferirle dicha energía potencial es necesario dotar al cuerpo de cierta velocidad inicial (la velocidad de escape)
Que dicha velocidad en términos energéticos se traduce en una energía cinética que se irá "consumiendo" a medida que el cuerpo se aleja, aumentando la energía potencial. En el infinito el cuerpo tendrá una energía potencial de cero julios y consideraremos que llega con velocidad cero (energía cinética también nula)
Que la energía mecánica se conserva en todo el proceso
Que la masa de la Tierra es M_T y su radio R_T y la masa del cuerpo que queremos situar en el infinito es m

A partir de lo anterior, podemos escribir:

$E_{m_{\infty}} = E_{m_{s u p}} \Rightarrow E_{p_{\infty}} + E_{c_{\infty}} = E_{p_{s u p}} + E_{c_{s u p}} \Rightarrow E_{p_{s u p}} = - E_{c_{s u p}} \Rightarrow \Rightarrow - G \cdot \frac{M_{T} \cdot m}{R_{T}} = - \frac{1}{2} \cdot m \cdot {v_{e}}^{2} \Rightarrow v_{e} = \sqrt{\frac{2 \cdot G \cdot M_{T}}{R_{T}}}$

Las conclusiones a las que hemos llegado no son sólo válidas para el caso de la Tierra si no que pueden extenderse para el campo generado por cualquier otro planeta o cuerpo esférico de masa M.

Definimos la velocidad de escape de un cuerpo como la mínima que debe comunicársele para que salga del campo gravitatorio generado por otro. Su valor, suponiendo que el cuerpo se encuentra inicialmente a una distancia R del planeta o cuerpo generador de campo, puede ser determinada por la expresión:

v_{e} = \sqrt{\frac{2 \cdot G \cdot M}{R}} = \sqrt{2 \cdot g \cdot R}

Donde:

v_e es la velocidad de escape. Su unidad de medida en el Sistema Internacional (S.I.) es el metro por segundo (m/s)
G es la constante de gravitación universal, que no depende de los cuerpos que interaccionan y cuyo valor es G = 6,67·10^-11 N·m²/kg²,
M es la masa del planeta o cuerpo que genera el campo gravitatorio. Su unidad de medida en el Sistema Internacional (S.I.) es el kilogramo (kg). En el caso del planeta Tierra, M = 5.972·10²⁴ kg
g es el valor de la intensidad de campo gravitatorio en el punto considerado. También se le conoce como aceleración de la gravedad. Su unidad de medida en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado (m/s²), equivalente al newton por kilogramo (N/kg).En el caso de la superficie de la Tierra g = g₀ = 9.8 m/s² = 9.8 N/kg
R es la distancia a la que se encuentra el cuerpo del centro del planeta o cuerpo generador de campo considerado. Su unidad de medida en el Sistema Internacional (S.I.) es el metro. En el caso de la superficie de la Tierra, R_T = 6371·10³ m

Velocidad de escape de la Tierra

El valor de la velocidad de escape para un cuerpo en la superficie terrestre es $v_{e} = \sqrt{2 \cdot 9.8 \cdot 6371 \cdot 10^{3}} = 11174.5 m / s = 11.17 k m / s$ . Este sería el valor con el el súper hombre de la figura anterior debería lanzar su balón si quisiera que abandonase la influencia del campo gravitatorio terrestre.

Observa las siguientes características:

Dicho valor es independiente de la dirección del lanzamiento, siempre que no apuntemos al suelo, claro está
No depende de la masa del cuerpo lanzado, es decir, la velocidad de escape de un cuerpo de 1 kg es la misma que la de un cuerpo de 1000 kg. ¿Contradice esto tu sentido común? Si lo piensas detenidamente g tampoco depende de la masa del cuerpo (todos los cuerpos caen con igual aceleración en el vacío, independientemente de su masa). Lo que si es cierto es que los cuerpos más pesados requieren de un trabajo mayor para alcanzar la velocidad de escape, es decir, cuesta más alcanzar 11.17 km/s con un cuerpo de 1000 kg que con uno de 1 kg
Dicha velocidad lleva asociada una energía cinética conocida como energía de amarre o ligadura ya que cualquier cuerpo cuya energía se encuentre por debajo de ella queda ligado o amarrado al campo. Su valor, para un cuerpo de 1 kg es: $E_{c} = \frac{1}{2} \cdot m \cdot {v_{e}}^{2} = \frac{1}{2} \cdot 1 \cdot {11174.5}^{2} = 6.24 \cdot 10^{7} J$ .

Finalmente, observa que en nuestro modelo hemos considerado que la Tierra es el único cuerpo que existe que crea un campo capaz de atraer al objeto lanzado. En el caso real de las sondas espaciales, por ejemplo, existen otros cuerpos celestes en el espacio: otros planetas y estrellas del Sistema Solar y fuera de él. El campo que crean se usa para impulsarlas aumentando su energía cinética en las proximidades de los mismos. A este proceso se le denomina asistencia gravitacional y está relacionado con el siguiente apartado, como veremos.

Ejemplo

Determina la velocidad de escape de un punto situado a 40000 km de altura respecto a la Tierra.

Datos: Radio de la Tierra: 6371 km; Masa terrestre: 5.97·10²⁴ kg

Ver solución

Cuerpos libres y ligados

El valor de la energía mecánica de un cuerpo en un campo gravitatorio nos puede servir para determinar si puede escapar a los efectos del mismo, en cuyo caso decimos que el cuerpo es libre, o no, en cuyo caso decimos que el cuerpo está ligado al campo. Efectivamente, la velocidad de escape, v_e, es una velocidad límite que marca, por extensión, el valor mínimo de energía mecánica para el abandono del campo. Recuerda que la energía mecánica se conserva cuando el cuerpo está sometido exclusivamente a la fuerza gravitatoria, por lo que es facilmente deducible de la propia definición de velocidad de escape que dicho valor límite corresponde a E_m = 0:

$E_{m_{\infty}} = E_{c_{\infty}} + E_{p_{\infty}} = E_{m_{s u p}} = E_{c_{s u p}} + E_{p_{s u p}} = \frac{1}{2} \cdot m \cdot {(\underset{v_{e}}{\underset{⏟}{\sqrt{\frac{2 \cdot G \cdot M}{R}}}})}^{2} - G \cdot \frac{M \cdot m}{R} = 0$

Por tanto:

Definimos un cuerpo libre de un campo gravitatorio como aquel que tiene su energía mecánica mayor que cero. En tal caso, el cuerpo no está ligado al campo. Observa que la energía potencial gravitatoria siempre es negativa y, por ello, $E_{m} \geq 0 \Rightarrow E_{c} \geq |E_{p}|$
Definimos un cuerpo ligado o cuerpo amarrado a un campo gravitatorio como aquel que tiene su energía mecánica menor que cero. En tal caso, el cuerpo no podrá escapar al campo. Dado que la energía potencial gravitatoria siempre es negativa se cumple que $E_{m} < 0 \Rightarrow E_{c} < |E_{p}|$

Interpretación gráfica

Las gráficas de la energía en función de la distancia al origen nos permiten profundizar y aclarar aún más el concepto de cuerpo libre y de cuerpo ligado al campo.

Energía del cuerpo libre

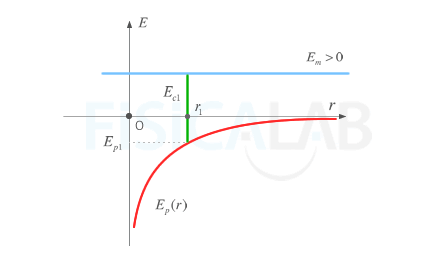
Componentes energéticas de un cuerpo libre

En la figura se representan las componentes energéticas de un cuerpo libre. Observa que la energía mecánica, mayor que cero, permanece constante a cualquier distancia r. A una determinada distancia r₁, el cuerpo cuenta con una energía potencial E_p1 y una energía cinética E_c1 que es la diferencia entre la energía mecánica y la energía potencial.

Energía del cuerpo ligado

Componentes energéticas de un cuerpo ligado

En la figura se representan las componentes energéticas de un cuerpo ligado a un campo. Observa que la energía mecánica, menor que cero, permanece constante a cualquier distancia r permitida. De nuevo la diferencia entre la energía mecánica E_m y la potencial E_p nos devuelve el valor de energía cinética E_c, como ocurre a una distancia r₁ con E_p1 y E_c1. Sin embargo, en este caso, el punto en el que se igualan la energía mecánica y la potencial nos da el valor máximo permitido de r (r_MAX). Dicho valor ocurre cuando toda la energía mecánica del cuerpo es potencial y por tanto la energía cinética será 0. Valores mayores de r implicarían una energía cinética negativa, lo cual es imposible por la propia definición de la misma.

Relación con la forma de las órbitas

El valor de energía que tiene un cuerpo determina la forma de las órbitas. Así:

Energía mecánica negativa. Se trata de cuerpos ligados al campo y que por tanto tienen órbitas cerradas elípticas o circulares

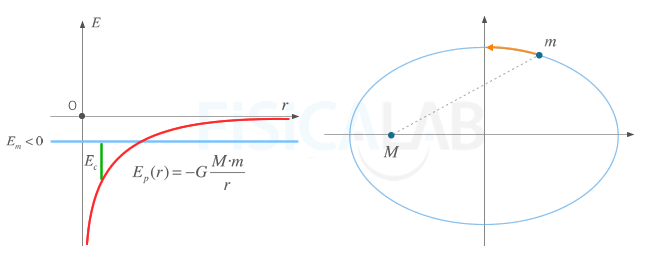
Energía mecánica negativa y las órbitas.

Aquellos cuerpos que tienen una energía mecánica negativa describen órbitas elípticas o circulares cuya extensión está condicionada por el punto de corte entre E_m y E_p.

Energía mecánica positiva. Se trata de cuerpos libres y por tanto tienen órbitas abiertas hiperbólicas

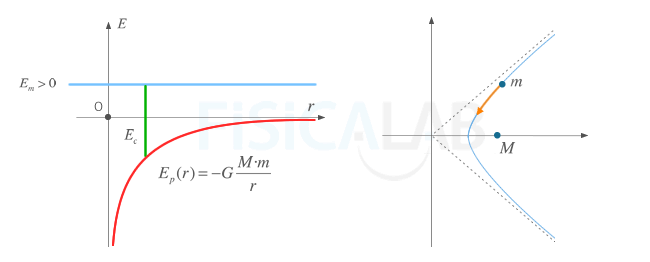
Energía mecánica positiva y las órbitas

Aquellos cuerpos que tienen una energía mecánica positiva describen órbitas hiperbólicas. En todo momento se cumple que E_c>|E_p|
Energía mecánica nula. Se trata de cuerpos libres, aunque están en el límite. Tienen órbitas abiertas parabólicas

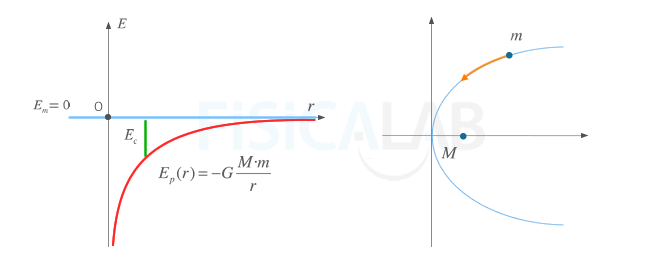
Distribución de energía mecánica a lo largo de una órbita elíptica

Energía mecánica nula y órbitas

Aquellos cuerpos que poseen una energía mecánica nula describen órbitas con forma de parábola.

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.