Potencial Gravitatorio
El potencial gravitatorio es, junto con la intensidad de campo gravitatorio, la magnitud que se utiliza para cuantificar el campo gravitatorio en un punto. A diferencia del primero, el potencial es una magnitud escalar. Mientras que la intensidad de campo es una magnitud útil para estudiar las fuerzas que aparecen en un cuerpo fruto de la acción gravitatoria, el potencial, como vamos a ver, es útil para estudiar la energía potencial que posee una partícula debido a esta. En este apartado veremos:
- El concepto de potencial gravitatorio y de diferencia de potencial gravitatorio
- La expresión del potencial gravitatorio creado por una masa puntual (o un cuerpo esférico) y sus propiedades
- El potencial gravitatorio creado por varias masas puntuales (o cuerpos esféricos)
- La relación que hay entre potencial e intensidad de campo gravitatorio
¿Empezamos?
Concepto de potencial gravitatorio
Imaginemos una masa m generadora de campo. Si situamos en sus proximidades una masa testigo m', esta contara con una determinada energía potencial gravitatoria. Al igual que ocurría con la fuerza gravitatoria, dicha energía es una magnitud que depende de la masa testigo, por lo que no es exclusiva del campo en sí. Sin embargo, a partir de ella podemos llegar al concepto de potencial y usarlo para cuantificar dicho campo, al igual que hacíamos con el concepto de intensidad de campo gravitatorio a partir de la citada fuerza gravitatoria.
El potencial gravitatorio en un punto es la energía potencial que la unidad de masa m' adquiere al ser colocada sobre dicho punto.
Donde:
- V es el potencial gravitatorio en un punto del campo gravitatorio. Su unidad de medida en el Sistema Internacional (S.I.) es el julio por kilogramo (J/kg)
- Ep es la energía potencial gravitatoria que adquiere una partícula testigo m' al situarla en ese punto.
El hecho de que todas las magnitudes sean escalares, permite que el estudio del campo gravitatorio sea más sencillo. De esta forma, si conocemos el valor del potencial gravitatorio V en un punto, podemos determinar que la energía potencial gravitatoria de una masa m situada en él es:
Diferencia de Potencial Gravitatorio
Si dos puntos de un campo gravitatorio poseen distinto potencial, entre ambos puntos existe lo que se denomina una diferencia de potencial, ΔV. Este valor se encuentra íntimamente relacionado con el trabajo gravitatorio. Por definición, el trabajo que realiza la fuerza gravitatoria para trasladar una masa m en el interior de un campo gravitatorio desde un punto A a otro B se obtiene, de acuerdo a lo ya visto en el apartado sobre energía potencial gravitatoria, por medio de la siguiente expresión:
Si aplicamos la definición de potencial gravitatorio, obtenemos que:
La diferencia de potencial gravitatorio entre dos puntos A y B de un campo gravitatorio es el opuesto del trabajo realizado por el campo para trasladar una unidad de masa desde el punto A al B.
Donde la unidad de medida en el Sistema Internacional de la diferencia de potencial gravitatorio es el julio por kilogramo (J/kg).
Potencial gravitatorio creado por una masa puntual
Una única partícula m es capaz de crear un campo gravitatorio a su alrededor. Si en dicho campo introducimos una masa testigo m' , entonces, aplicando la definición de potencial gravitatorio y atendiendo a la definición de energía potencial gravitatoria de dos masas puntuales, nos quedaría que:
El potencial gravitatorio del campo gravitatorio creado por una masa puntual m se obtiene por medio de la siguiente expresión:
Donde:
- V es el potencial gravitatorio en un punto. Su unidad de medida en el Sistema Internacional ( S.I. ) es el julio por kilogramo ( J/kg )
- G es la constante de gravitación universal. Su valor es G = 6.67·10-11 N·m2/kg2
- m es la masa puntual que crea el campo gravitatorio. Su unidad de medida en el Sistema Internacional ( S.I ) es el kilogramo ( kg )
- r es la distancia entre la masa y el punto donde medimos el potencial. En el Sistema Internacional ( S.I. ) se mide en metros (m).
La expresión anterior también es válida para el potencial que genera una masa esférica, siempre que r > R, siendo R el radio de la esfera.
Propiedades
El potencial de campo gravitatorio creado por una masa puntual o una masa esférica de radio R tiene las siguientes propiedades:
- Depende de la masa que lo crea y es independiente de la masa o masas a las que pueda afectar
- Su valor, como ocurre con la energía potencial, es negativo a una distancia genérica de la masa y aumenta de forma inversamente proporcional a esta hasta llegar a un valor máximo de 0 a una distancia infinita
- Su valor es el mismo para todas las partículas que se sitúan a una determinada distancia de la masa generadora. Dicho con otras palabras: tiene simetría esférica

Potencial Gravitatorio
A medida que nos alejamos de la masa generadora de campo el potencial gravitatorio, cuyo valor depende de la masa generadora, aumenta. En el infinito el potencial, al igual que la energía potencial gravitatoria, es cero.
Potencial gravitatorio creado por varias masas
Si el campo gravitatorio es creado por varias masas puntuales, el potencial gravitatorio en un punto sigue el principio de superposición:
El potencial gravitatorio originado por n masas puntuales en un punto de un campo gravitatorio es la suma escalar de los potenciales gravitatorios en dicho punto creados por cada una de las n masas por separado.
O lo que es lo mismo:
Potencial Gravitatorio
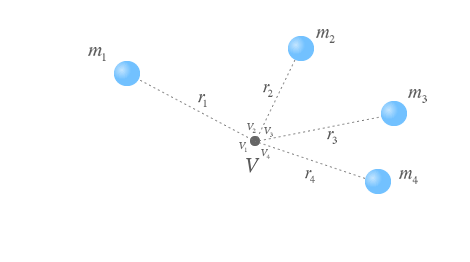
Podemos obtener el potencial gravitatorio generado por un conjunto de partículas en un punto sumando las contribuciones de cada uno de los potenciales que crea cada partícula por si sola. De esta forma en el punto gris de la figura, el potencial corresponde con:
V = V1 + V2 + V3 + V4
La expresión anterior también es válida para el potencial que genera un conjunto de masas esféricas.
Relación con la intensidad de campo
Si consideramos el módulo de la intensidad de campo gravitatorio, podemos comprobar que está estrechamente relacionado con el valor del potencial gravitatorio:
Sin embargo en esta observación, no hemos tenido en cuenta que la intensidad de campo
Aunque una comprobación más rigurosa queda fuera del alcance de este nivel, y dado que, en general, V depende de x, y y z, podemos analizar como varía V en función de x dejando fijas y y z. Esta variación será la componente x de la intensidad de campo
En un campo gravitatorio, la intensidad del campo en función del potencial se puede obtener por medio de la siguiente expresión:
O también:
Donde:
- El operador ∂ indica derivada parcial y se utiliza igual que el operador derivada d, salvo que sobre funciones que dependen de varias variables, como es el caso de V. Así, cuando derivamos respecto a una variable,por ejemplo respecto a x, trataremos el resto, en nuestro ejemplo, y y z, como si fueran constantes
En ocasiones resulta también de utilidad seguir un camino complementario al anterior que nos permita conocer la diferencia de potencial a partir de la intensidad de campo. Para ello partiremos de la definición de diferencia de potencial obtenida anteriormente y aplicaremos la expresión del trabajo gravitatorio:
Superficies equipotenciales
Aquellos puntos contiguos donde el valor del potencial gravitatorio es el mismo, reciben el nombre de superficies equipotenciales. Cada punto de una superficie equipotencial se caracteriza porque:
- El campo gravitatorio, también conocido como intensidad de campo gravitatorio
- Cada punto solo puede pertenecer a una superficie equipotencial, ya que el potencial eléctrico es un único valor en cada punto
En la siguiente imagen están representadas algunas superficies equipotenciales y lineas de campo de una masa puntual genérica.
Superficies Equipotenciales
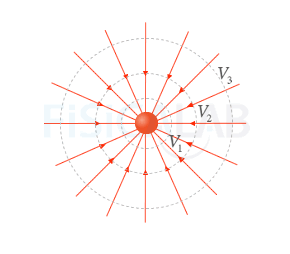
Las círcunferencias concéntricas de la figura son la representación de las superficies equipotenciales. En cada punto de cada una de ellas el potencial tiene el mismi valor, decreciente a medida que la circunferencia está más próxima a la masa generadora (V1 < V2 < V3). Por otro lado, la intensidad de campo gravitatorio, representada en la imagen por las flechas concéntricas, siempre es perpendicular a las superficies equipotenciales y apuntan hacia potenciales decrecientes.
Si lo deseas puedes ampliar información sobre otras formas de representar el campo gravitatorio.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
