Leyes de Kepler

Las leyes de Kepler surgen para explicar matemáticamente el movimiento de los planetas alrededor del Sol. Se pueden considerar las precursoras de la Ley de la gravitación universal de Newton. En este apartado vamos a estudiar:

Una breve introducción histórica
La primera ley de Kepler
La segunda ley de Kepler, donde veremos qué es la velocidad areolar, el perihelio y el afelio
La tercera ley de Kepler
Bajo que circunstacias podemos usarlas

¿Estás preparado?

Contexto histórico

Desde la Antigüedad clásica los filósofos, matemáticos y astrónomos griegos trataron de explicar el movimiento de los planetas y las estrellas tal y como los vemos desde la Tierra. Existían dos modelos para describir dicho movimiento:

Sistema geocéntrico: La Tierra se encontraba en el centro del Universo y, alrededor, el resto de astros. La mayoría de los filósofos griegos como Platón, Aristóteles o Ptolomeo defendían este modelo
Sistema heliocéntrico: El Sol se encontraba en el centro del Universo y, alrededor, la Tierra y el resto de astros. Galileo fue, en el S. XVII, el principal difusor de esta teoría, basándose en trabajos realizados por Nicolás Copérnico

Ambos sistemas se basaban en la idea de que los cuerpos celestes siempre se movían según el movimiento circular uniforme. Pero tenían que recurrir a complicadas sumas de trayectorias circulares (epiciclos y deferentes) para explicar las observaciones desde la Tierra.

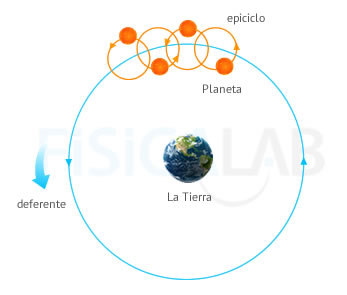
La Tierra como centro del universo. El sol realiza movimientos epiciclos y deferentes

Sistema Geocéntrico

Ptolomeo explica sus observaciones recurriendo a los epiciclos, representados en naranja y a los deferentes, en color azul. Copérnico también recurre a ellos, aunque los emplea de manera mucho más limitada

En el año 1600 un joven Johannes Kepler (1571 - 1630) fue a trabajar como ayudante matemático de Tycho Brahe (1546 - 1601), quién había estado recopilando exhaustivamente datos astronómicos sobre la posición de los planetas en el cielo. A la muerte de Brahe, y a partir de los datos recopilados, Kepler intentó obtener la órbita circular de Marte. Sin embargo ningún círculo se ajustaba a las medidas de Tycho. En lugar de círculos, Kepler encontró que utilizando elipses el ajuste con las observaciones era perfecto. Así surgieron las leyes de Kepler.

Kepler no comprendió el origen de sus leyes. Fue Newton, años más tarde, quien describió con precisión las magnitudes que permitían explicarlas, enunciando así la ley de la gravitación universal.

Primera ley de Kepler: ley de las órbitas

La primera ley, conocida como ley de las órbitas, acaba con la idea, mantenida también por Copernico, de que las órbitas debían ser circulares.

Los planetas giran alrededor del Sol siguiendo una trayectoria elíptica. El Sol se sitúa en uno de los focos de la elipse.

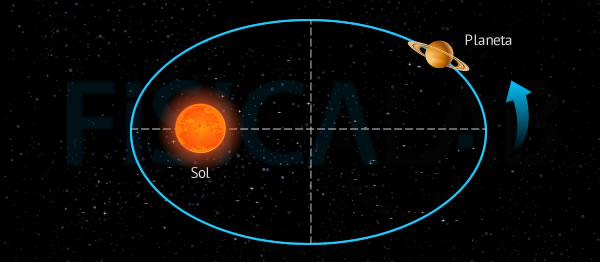
Planeta describiendo un órbita elíptica alrededor del Sol

Primera Ley de Kepler

La primera ley de Kepler establece que todos los planetas se mueven alrededor del Sol describiendo una trayectoria elíptica.

La excentricidad e de una elipse es una medida de lo alejado que se encuentran los focos del centro. Su valor viene dado por:

$e = \sqrt{1 - \frac{b^{2}}{a^{2}}}$

Pues bien, la mayoría de las órbitas planetarias tienen un valor muy pequeño de excentricidad, es decir e ≈ 0. Esto significa que, a nivel práctico, pueden considerarse círculos descentrados.

Experimenta y Aprende

Datos
a = | b =

Excentricidad de una elipse

La figura muestra una elipse con el semieje mayor horizontal (a) y el semieje menor vertical (b). Puedes arrastrar el valor de su excentricidad y al hacerlo cambiarás el valor de la longitud de sus semiejes a y b. De igual forma puedes mover el punto origen O (x₀ , y₀). Observa como a medida que la excentricidad se aproxima a 0, la longitud de a se iguala a la de b, obteniendo poco a poco una circunferencia.

Por esta razón podemos considerar la circunferencia como un caso particular de la elipse en el que los semejes mayor y menor coinciden a = b.

Segunda ley de Kepler: Ley de las áreas

La segunda ley, conocida como ley de las áreas, nos da información sobre la velocidad a la que se desplaza el planeta.

La recta que une el planeta con el Sol barre áreas iguales en tiempos iguales.

Para que esto se cumpla, la velocidad del planeta debe aumentar a medida que se acerque al Sol. Esto sugiere la presencia de una fuerza que permite al Sol atraer los planetas, tal y como descubrió Newton años más tarde.

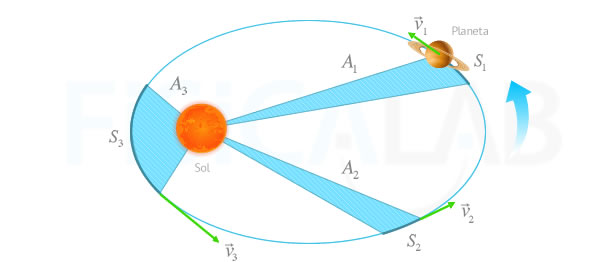
Planeta describiendo una órbita elíptica alrededor del Sol pero mostrando que en el mismo tiempo el planeta siempre describe áreas iguales.

Segunda Ley de Kepler

Suponiendo que el tiempo que se tarda en recorrer un espacio S₁, S₂ y S₃ es el mismo, las áreas A₁, A₂ y A₃ también serán iguales. Esto se debe a que a medida que disminuye la distancia al Sol, la velocidad aumenta (v₁ < v₂ < v₃)

Velocidad areolar

Se define la velocidad areolar v_A como el área barrida por el vector de posición de un cuerpo por unidad de tiempo. Según la segunda ley de Kepler, v_A es constante. Por tanto:

v_{A} = \frac{d A}{d t} = cte

En un instante, es decir, un diferencial de tiempo dt, el planeta se desplaza $d \vec{r} = \vec{v} \cdot d t$ . Ya que se trata de un diferencial podemos considerar que $d \vec{r}$ es una línea recta. Pues bien, los vectores $\vec{r}$ y $d \vec{r}$ determinan un paralelogramo cuya área es justo el doble que dA. En la siguiente imagen puedes observar el área correspondiente a dA, que supone la mitad de la del hipotético paralelogramo.

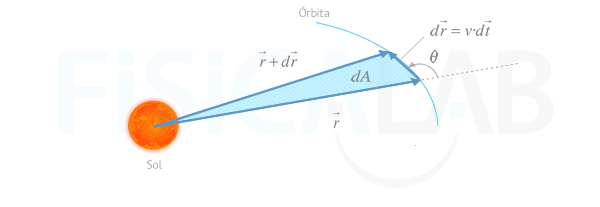
Diferencial de posición de la órbita de un planeta

Estudio de un diferencial del área

Recuerda que el módulo del producto vectorial de dos vectores es justamente el área del paralelogramo que forman. Así, nos queda:

$v_{A} = \frac{d A}{d t} = \frac{\frac{1}{2} \cdot |\vec{r} \times d \vec{r}|}{d t} \underset{[1]}{=} \frac{1}{2} \cdot |\vec{r} \times \vec{v}| \underset{[2]}{=} \frac{1}{2} \cdot r \cdot v \cdot \sin (θ) = cte [1] \vec{v} = \frac{d \vec{r}}{d t} [2] |\vec{r} \times \vec{v}| = r \cdot v \cdot \sin (θ)$

La segunda ley de Kepler establece que la velocidad areolar v_A permanece constante a lo largo del recorrido del planeta. Por ello, dados dos puntos de la trayectoria cualesquiera, nos queda:

r_{1} \cdot v_{1} \cdot \sin (θ_{1}) = r_{2} \cdot v_{2} \cdot \sin (θ_{2})

Donde:

r₁ y r₂: Módulos de los vectores de posición del planeta en los puntos 1 y 2 respectivamente. Su unidad de medida en el Sistema Internacional es el metro (m)
v₁ y v₂ : Módulos de los vectores velocidad del planeta en los puntos 1 y 2 respectivamente. Su unidad de medida en el Sistema Internacional es el metro por segundo ( m/s)
θ₁ y θ₂: Ángulos que forman los vectores de posición de los planetas con los de velocidad en los puntos 1 y 2 respectivamente. Su unidad de medida en el Sistema Internacional es el radián ( rad )

En definitiva, aunque la velocidad areolar v_A sí permanece constante en todo el recorrido, para que se cumpla la segunda ley de Kepler la velocidad instantánea del planeta debe variar según el punto de su trayectoria en que se encuentre y el ángulo θ que formen $\vec{r}$ y $\vec{v}$ .

Además, si la trayectoria de un planeta fuese aproximadamente circular ( excentricidad e ≈ 0 ), θ = 90º en cualquier punto y v₁ = v₂ , es decir, estaríamos ante un movimiento circular uniforme.

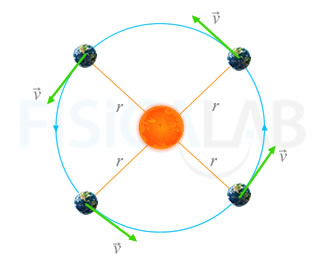
Cuando las órbitas de los planetas alrededor se consideran circulares la velocidad es constante

Movimiento Circular Uniforme

Cuando la excentricidad de la órbita del planeta es mínima (e ≈ 0), se encuentra siempre a la misma distancia del Sol y por tanto su velocidad se puede considerar constante. De ahí que el movimiento descrito por este sea un m.c.u.

Perihelio y afelio

Perihelio: Es el punto de la órbita del planeta más próximo al Sol. La velocidad en las proximidades del perihelio es la máxima.
Afelio: Es el punto de la órbita del planeta más lejano al Sol. La velocidad en las proximidades del afelio es la mínima.

En el perihelio (p) y en el afelio (a) θ = 90º y por tanto:

r_{a} \cdot v_{a} = r_{p} \cdot v_{p}

Tercera ley de Kepler: Ley de los periodos

La tercera ley, también conocida como armónica o de los periodos, relaciona los periodos de los planetas, es decir, lo que tardan en completar una vuelta alrededor del Sol, con sus radios medios.

Para un planeta dado, el cuadrado de su periodo orbital es proporcional al cubo de su distancia media al Sol. Esto es,

T^{2} = k \cdot r^{3}

Donde:

T : Periodo del planeta. Su unidad de medida en el Sistema Internacional es el segundo ( s )
k : Constante de proporcionalidad. Su unidad de medida en el Sistema Internacional es el segundo al cuadrado partido metro cúbico ( s²/m³)
r : Distancia media al Sol. Por las propiedades de la elipse se cumple que su valor coincide con el del semieje mayor de la elipse, a. Su unidad de medida en el Sistema Internacional es el metro ( m )

Observa que como consecuencia de esta ley, los planetas se mueven tanto más despacio cuanto mayor es su órbita. El valor concreto de la constante k será estudiado cuando hayamos introducido la ley de la gravedad formalmente. De momento si que señalaremos que su valor es el mismo para todos aquellos cuerpos que giran en torno a uno determinado. Así, por ejemplo, los planetas del Sistema Solar comparten el valor de k al girar todos ellos alrededor del Sol. También los satélites de un planeta compartirán un valor de k entre ellos.

Es por ello que, en ocasiones, esta ley se presenta de acuerdo a la siguiente expresión:

\frac{{T_{1}}^{2}}{{T_{2}}^{2}} = \frac{{r_{1}}^{3}}{{r_{2}}^{3}} = \frac{{a_{1}}^{3}}{{a_{2}}^{3}}

Donde los subíndices 1 y 2 indican los periodos ( T ) , distancias medias ( r ) y longitud del semieje mayor (a = r ) de las órbitas de dos cuerpos que giran en torno a uno común, por ejemplo, dos planetas cualesquiera alrededor del Sol.

Finalmente, calcular la longitud de la elipse requiere de herramientas matemáticas que están fuera del alcance de este nivel. Sin embargo, para valores de excentricidad pequeños ( e ≈ 0 ), su longitud viene a ser aproximadamente igual a la de un círculo que tuviese como radio el radio medio de la elipse asociada, es decir, el semeje mayor a. Tal y como dijimos cuando hablamos de la primera ley, las órbitas de los planetas, al tener una excentricidad pequeña, se pueden considerar círculos descentrados.

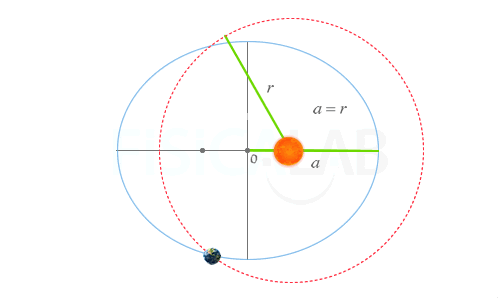
Valor del radio medio de una elipse

La distancia media r de un planeta al foco de su órbita (ocupado por el Sol) coincide con la longitud del semieje mayor a de la elipse. Consideraremos este valor a la hora de determinar la longitud de la elipse cuando esta tenga una excentricidad pequeña. Así, en la figura, podríamos aproximar la longitud de la elipse, en verde, por la del círculo en rojo siendo L_elipse ≅ L_circunf. = 2·π·r=2·π·a.

¿Cuándo se pueden usar las leyes de Kepler?

Kepler dedujo estas tres leyes a partir de la observación del movimiento de los planetas alrededor del Sol, y por ello, a lo largo de este apartado hemos enunciado las leyes en relación al Sol y a los planetas. Sin embargo, gracias a ellas podemos estudiar también:

El movimiento de cualquier cuerpo que orbite alrededor del Sol:
- planetas
- asteroides
- cometas
Satélites orbitando alrededor de planetas
- Naturales ( por ejemplo, la Luna )
- Artificiales

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.